Question

直角三角形的三邊長是3、4、5厘米，以斜邊所在直線為軸旋轉，形成一立體圖形，試求該立體圖形的體積．

Answer 1

解：直角三角形斜邊所在直線為軸旋轉一周，得到的幾何體是同一底面的兩個圓錐，如上圖所示，
設這個圓錐的底面半徑是r，則：
5r÷2=3×4÷2，
5r=12，
r=2.4，
所以這個立體圖形的體積是：
×3.14×2.4²×（AO+CO），
=×3.14×5.76×5；
=30.114（立方厘米），
答：旋轉一周后的立體圖形的體積是30.114立方厘米．
分析：直角三角形斜邊所在直線為軸旋轉一周，得到的幾何體是同一底面的兩個圓錐，用直角三角形的面積求出底面圓的半徑，然后用圓錐的體積公式求出幾何體的體積．

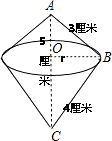
點評：本題考查的是圓錐的計算，以直角三角形斜邊所在的直線為軸轉動一周，得到的幾何體是兩個圓錐，用圓錐的體積公式求出這個幾何體的體積．