(1)在一個不透明的袋子里裝有形狀、大小都相同的4支黃粉筆、3支白粉筆和1支綠粉筆.任意摸一支,摸到______粉筆的可能性最大,是______%;摸到______粉筆的可能性最小,是______;,摸到白粉筆的可能性是______.
(2)桌上擺著20張卡片,分別寫著1~20各數,如果摸到一位數小明獲勝,摸到兩位數小方獲勝,______獲勝的可能性大.小明獲勝的可能性是______,小方獲勝的可能性是______.
解:(1)黃粉筆:4÷(4+3+1),
=4÷8,
=50%,
白粉筆:3÷(4+3+1),
=3÷8,
=37.5%,
綠粉筆:1÷(4+3+1),
=1÷8,
=12.5%,
因為:50%>37.5%>12.5%,所以摸到黃色粉筆的可能性最大,是50%,摸到綠粉筆的可能性最小,是12.5%,摸到白粉筆的可能是37.5%;
(2)在1~20中,一位數有1~9共9個,兩位數有10~20共11個,
小明獲勝的可能性是:9÷20=

,
小方獲勝的可能性是:11÷20=
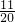
,
因為:
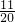
>

,所以小方獲勝的可能性大,小明獲勝的可能性是
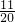
,小方獲勝的可能性是

;
故答案為:黃,50,綠,12.5%,37.5%,小方,

,
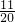
.
分析:(1)先求出袋子中粉筆的總支數,進而根據可能性的計算方法,用除法分別求出摸出各種顏色粉筆的可能性,然后比較即可;
(2)在1~20中,一位數有1~9共9個,兩位數有10~20共11個,根據可能性的計算方法,用除法分別求出摸到一位數和二位數的可能性,然后比較即可.
點評:解答此題應根據可能性的求法:即求一個數是另一個數的幾分之幾用除法解答,進而得出結論.

 ,
,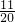 ,
,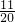 >
> ,所以小方獲勝的可能性大,小明獲勝的可能性是
,所以小方獲勝的可能性大,小明獲勝的可能性是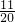 ,小方獲勝的可能性是
,小方獲勝的可能性是 ;
; ,
,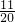 .
.

 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案 摸出紅球的可能性是
摸出紅球的可能性是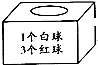 摸出紅球的可能性是
摸出紅球的可能性是 摸出紅球的可能性是______;摸出黃球的可能性是______
摸出紅球的可能性是______;摸出黃球的可能性是______ 摸出紅球的可能性是______;摸出白球的可能性是______
摸出紅球的可能性是______;摸出白球的可能性是______