Question

如圖所示，擺放小正方體．
（1）當擺到第七層時一共有

 

個小正方體．
（2）當擺放到n層時一共

 

個正方體．

Answer 1

考點：數與形結合的規律

專題：探索數的規律

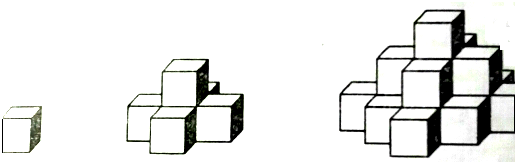
分析：圖（1）中只有一層，有（4×0+1）一個正方形，圖（2）中有兩層，在圖（1）的基礎上增加了一層，第二層有（4×1+1）個．圖（3）中有三層，在圖（2）的基礎長增加了一層，第三層有（4×2+1），依此類推當圖形有二層和七層時總的正方形的個數．
依此類推總結規律當有n層時總的正方體個數．

解答： 解：根據分析：當圖形有二層時，第二層的正方形個數為：（4×1+1），則此時總的正方形個數為1+（4×1+1）=6；
當圖形有七層時，第七層的個數為：（4×6+1），
則此時總的正方形個數為：1+（4×1+1）+（4×2+1）+（4×3+1）+（4×4+1）+（4×5+1）+（4×6+1）=91．
歸納可知，第n個疊放圖形中共有n層，構成了以1為首項，以4為公差的等差數列
所以S_n=n+

n(n-1)×4

=2n²-n
故答案為：91，2n²-n．

點評：本題主要考查歸納推理，其基本思路是先分析具體，觀察，總結其內在聯系，得到一般性的結論，若求解的項數較少，可一直推理出結果，若項數較多，則要得到一般求解方法，再求具體問題．