解:(1)13+23+33+43+53=1+8+27+64+125=225;
(1+2+3+4+5)2=152=225;
所以13+23+33+43+53=(1+2+3+4+5)2.
(2)結合圖形:大正方形的面積等于所有小正方形的面積之和為:
52×20+42×16+32×12+22×8+12×4,
=52×5×4+42×4×4+32×3×4+22×2×4+12×1×4,
=53×4+43×4+33×4+23×4+13×4,
=(53+43+33+23+13)×4;
同時,大正方形的邊長為:(1+2+3+4+5)×2,
所以面積為:
[1+2+3+4+5)×2]×[1+2+3+4+5)×2],
=[(1+2+3+4+5)×2]2
=(1+2+3+4+5)2×22,
=(1+2+3+4+5)2×4;
所以:(53+43+33+23+13)×4=(1+2+3+4+5)2×4;
即:13+23+33+43+53=(1+2+3+4+5)2.
(3)由以上結論猜想得出:
13+23+33+…+n3=(1+2+3+…+n)2.
故答案為:(1)=;猜想:(1+2+3+…+n)2.
分析:(1)通過計算判斷大小.
(2)根據所給圖形的面積證明(1)的判斷.
(3)根據以上兩個題的計算和驗證結論來推導.
點評:解決本題的關鍵是根據所給圖形的面積間的關系來推導出公式.

 探索:
探索:

 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案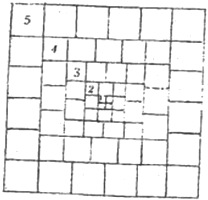 探索:
探索: