82
分析:根據題干可知,第1個圖形中小圓點的個數為10個,可以寫成10=(1+2)2+1;第2個圖形中小圓點的個數為17個,可以寫成17=(2+2)2+1;第3個圖形中小圓點的個數為26個,可以寫成26=(3+2)2+1;…由此第n個圖形中的小圓點個數就可以寫成:(n+2)2+1;由此即可解決問題.
解答:根據題意分析可得:第1個圖形中小圓點的個數為:10=(1+2)2+1;
第2個圖形中小圓點的個數為:17=(2+2)2+1;
第3個圖形中小圓點的個數為:26=(3+2)2+1;
…
第n個圖形中的小圓點的個數為:(n+2)2+1;
所以第7個圖形中小圓點的個數為:(7+2)2+1,
=81+1,
=82(個);
答:第7個圖形中小圓點的個數為82個.
故答案為:82.
點評:本題是一道找規律的題目,對于找規律的題目首先應找出哪些部分發生了變化,是按照什么規律變化的,并從已知的特殊個體推理得出一般規律.即可解決此類問題.

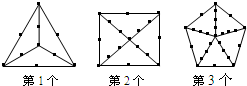 觀察下列各圖中小圓點的擺放規律,按這樣的規律繼續擺放下去,則第7個圖形中小圓點的個數為________.
觀察下列各圖中小圓點的擺放規律,按這樣的規律繼續擺放下去,則第7個圖形中小圓點的個數為________.

 小學課時特訓系列答案
小學課時特訓系列答案