考點：數與形結合的規律
專題：探索數的規律
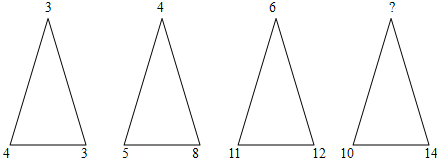
分析：首先分別求出每個三角形上面的頂點和右下角的頂點的兩個數的和；然后根據前三個三角形上面的頂點和右下角的頂點的兩個數的和的情況，總結出它們之間的關系，進而求出第四個三角形上面的頂點和右下角的頂點的兩個數的和，再減去14，求出上面的頂點代表的數字是多少即可．
解答：
解：根據分析，
第一個三角形上面的頂點和右下角的頂點的兩個數的和是：3+3=6；
第二個三角形上面的頂點和右下角的頂點的兩個數的和是：4+8=12；
第三個三角形上面的頂點和右下角的頂點的兩個數的和是：6+12=18；
因為12÷6=2，18÷6=3，
所以第二個三角形上面的頂點和右下角的頂點的兩個數的和是第一個的2倍，
所以第三個三角形上面的頂點和右下角的頂點的兩個數的和是第一個的3倍，
因此第四個三角形上面的頂點和右下角的頂點的兩個數的和是第一個的4倍，
可得？=6×4-14=10．
故答案為：10．
點評：此題主要考查了數形結合的規律，注意觀察總結出規律，并能正確應用．
長江作業本同步練習冊系列答案