
 兩個同樣大小的正方體形狀的積木.每個正方體上相對的兩個面上寫的數之和都等于9.現將兩個正方體并列放置.看得見的五個面上的數字如圖所示,則看不見的七個面上的數的和等于________.
兩個同樣大小的正方體形狀的積木.每個正方體上相對的兩個面上寫的數之和都等于9.現將兩個正方體并列放置.看得見的五個面上的數字如圖所示,則看不見的七個面上的數的和等于________.

 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:小學數學 來源: 題型:
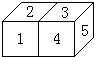 兩個同樣大小的正方體形狀的積木.每個正方體上相對的兩個面上寫的數之和都等于9.現將兩個正方體并列放置.看得見的五個面上的數字如圖所示,則看不見的七個面上的數的和等于
兩個同樣大小的正方體形狀的積木.每個正方體上相對的兩個面上寫的數之和都等于9.現將兩個正方體并列放置.看得見的五個面上的數字如圖所示,則看不見的七個面上的數的和等于查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com