
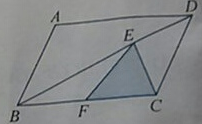
 如圖,已知平行四邊形ABCD的面積為54平方厘米,BE=2ED,BF=FC,求△EFC的面積.
如圖,已知平行四邊形ABCD的面積為54平方厘米,BE=2ED,BF=FC,求△EFC的面積. 分析 因為BD是對角線,所以三角形BDC的面積是平行四邊形面積的一半,因為BE=2ED,所以三角形BEC的面積是$\frac{2}{3}$,由此求出三角形BEC的面積,因為BF=FC,所以△EFC的面積是三角形BEC的面積的$\frac{1}{2}$,由此根據一個數乘分數的意義,用乘法即可求出△EFC的面積.
解答 解:54÷2×$\frac{2}{3}$×$\frac{1}{2}$
=18×$\frac{1}{2}$
=9(平方厘米)
答:△EFC的面積的9平方厘米.
點評 此圖考查了組合圖形的面積,明確在高一定時,三角形的底的比即面積的比;用到的知識點:三角形的面積計算公式.


科目:小學數學 來源: 題型:選擇題
| A. | 145 厘米 | B. | 138 厘米 | C. | 135 厘米 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com