
【題目】已知![]() 是定義在
是定義在![]() 上的偶函數(shù),當
上的偶函數(shù),當![]() 時,
時,![]() .
.
(1)用分段函數(shù)形式寫出![]() 的解析式;
的解析式;
(2)寫出![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)求出函數(shù)的最值.
【答案】(1)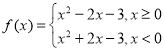 ;(2)
;(2)![]() 的增區(qū)間為
的增區(qū)間為![]() ,
,![]() ,減區(qū)間為
,減區(qū)間為![]() ,
,![]() ;(3)最小值為-4,無最大值.
;(3)最小值為-4,無最大值.
【解析】
(1)根據(jù)![]() 是定義在
是定義在![]() 上的偶函數(shù),且當
上的偶函數(shù),且當![]() 時,
時,![]() ,
,
設(shè)![]() ,則
,則![]() ,通過
,通過![]() 求解.
求解.
(2)每一段都是二次函數(shù),根據(jù)二次函數(shù)的圖象和性質(zhì)求解.
(3)利用(2)的單調(diào)性求解.
(1)![]() 是定義在
是定義在![]() 上的偶函數(shù),
上的偶函數(shù),
當![]() 時,
時,![]() ,
,
![]() 當
當![]() 時,設(shè)
時,設(shè)![]() ,則
,則![]() ,
,
![]()
![]()
即![]() 時,
時,![]() .
.
故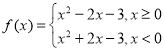 .
.
(2)如圖所示:
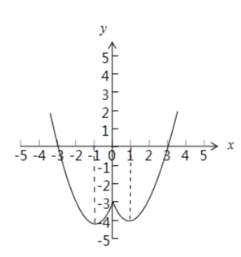
當![]() 時,
時,![]() ,對稱軸為
,對稱軸為![]() ,
,
![]() 增區(qū)間為
增區(qū)間為![]() ,減區(qū)間為
,減區(qū)間為![]() ;
;
當![]() 時,
時,![]() ,對稱軸為
,對稱軸為![]() ,
,
![]() 增區(qū)間為
增區(qū)間為![]() ,減區(qū)間為
,減區(qū)間為![]() .
.
綜上,![]() 的增區(qū)間為
的增區(qū)間為![]() ,
,![]() ,減區(qū)間為
,減區(qū)間為![]() ,
,![]() .
.
(3)由(2)知,當![]() 時,
時,![]() ,
,
![]() ,無最大值;
,無最大值;
當![]() 時,
時,![]() ,
,
![]() ,無最大值.
,無最大值.
綜上,函數(shù)的最小值為-4,無最大值.


 海淀課時新作業(yè)金榜卷系列答案
海淀課時新作業(yè)金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地有兩個國家AAAA級景區(qū)—甲景區(qū)和乙景區(qū).相關(guān)部門統(tǒng)計了這兩個景區(qū)2019年1月至6月的客流量(單位:百人),得到如圖所示的莖葉圖.關(guān)于2019年1月至6月這兩個景區(qū)的客流量,下列結(jié)論正確的是( )
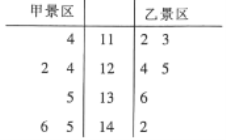
A.甲景區(qū)客流量的中位數(shù)為13000
B.乙景區(qū)客流量的中位數(shù)為13000
C.甲景區(qū)客流量的平均值比乙景區(qū)客流量的平均值小
D.甲景區(qū)客流量的極差比乙景區(qū)客流量的極差大
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
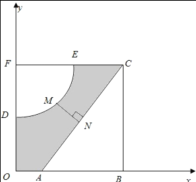
【題目】如圖,河的兩岸分別有生活小區(qū)![]() 和
和![]() ,其中
,其中![]() ,
,![]() 三點共線,
三點共線,![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,測得
,測得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,若以
,若以![]() 所在直線分別為
所在直線分別為![]() 軸建立平面直角坐標系
軸建立平面直角坐標系![]() 則河岸
則河岸![]() 可看成是曲線
可看成是曲線![]() (其中
(其中![]() 是常數(shù))的一部分,河岸
是常數(shù))的一部分,河岸![]() 可看成是直線
可看成是直線![]() (其中
(其中![]() 為常數(shù))的一部分.
為常數(shù))的一部分.
(1)求![]() 的值.
的值.
(2)現(xiàn)準備建一座橋![]() ,其中
,其中![]() 分別在
分別在![]() 上,且
上,且![]() ,
,![]() 的橫坐標為
的橫坐標為![]() .寫出橋
.寫出橋![]() 的長
的長![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式
的函數(shù)關(guān)系式![]() ,并標明定義域;當
,并標明定義域;當![]() 為何值時,
為何值時,![]() 取到最小值?最小值是多少?
取到最小值?最小值是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
, ![]() 為自然對數(shù)的底數(shù)),且曲線
為自然對數(shù)的底數(shù)),且曲線![]() 在點
在點![]() 處的切線平行于
處的切線平行于![]() 軸.
軸.
(1)求![]() 的值;
的值;
(2)求函數(shù)![]() 的極值.
的極值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過
,過![]() 且垂直于
且垂直于![]() 軸的焦點弦的弦長為
軸的焦點弦的弦長為![]() ,過
,過![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() ,
,![]() 互相垂直,直線
互相垂直,直線![]() 過
過![]() 且與橢圓
且與橢圓![]() 交于點
交于點![]() ,
,![]() 兩點,直線
兩點,直線![]() 過
過![]() 且與橢圓
且與橢圓![]() 交于
交于![]() ,
,![]() 兩點.求
兩點.求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我們在求高次方程或超越方程的近似解時常用二分法求解,在實際生活中還有三分法.比如借助天平鑒別假幣.有三枚形狀大小完全相同的硬幣,其中有一假幣(質(zhì)量較輕),把兩枚硬幣放在天平的兩端,若天平平衡,則剩余一枚為假幣,若天平不平衡,較輕的一端放的硬幣為假幣.現(xiàn)有 27 枚這樣的硬幣,其中有一枚是假幣(質(zhì)量較輕),如果只有一臺天平,則一定能找到這枚假幣所需要使用天平的最少次數(shù)為( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
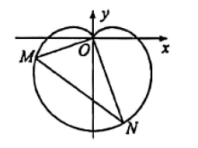
【題目】在新中國成立70周年國慶閱兵慶典中,眾多群眾在臉上貼著一顆紅心,以此表達對祖國的熱愛之情,在數(shù)學(xué)中,有多種方程都可以表示心型曲線,其中有著名的笛卡爾心型曲線,如圖,在直角坐標系中,以原點O為極點,x軸正半軸為極軸建立極坐標系.圖中的曲線就是笛卡爾心型曲線,其極坐標方程為![]() (
(![]() ),M為該曲線上的任意一點.
),M為該曲線上的任意一點.
(1)當![]() 時,求M點的極坐標;
時,求M點的極坐標;
(2)將射線OM繞原點O逆時針旋轉(zhuǎn)![]() 與該曲線相交于點N,求
與該曲線相交于點N,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com