--文科數(shù)學.files/image100.jpg)
19.解:(1)連接B1D1,ABCD―A1B1C1D1為四棱柱,
--文科數(shù)學.files/image102.gif) ,
,
則在四邊形BB1D1D中(如圖),
--文科數(shù)學.files/image104.gif)
得△D1O1B1≌△B1BO,可得∠D1O1B1=∠OBB1=90°,
即D1O1⊥B1O
(2)解法一:連接OD1,△AB1C,△AD1C均為等腰
三角形,
且AB1=CB1,AD1=CD1,所有OD1⊥AC,B1O⊥AC,
顯然:∠D1OB1為所求二面角D1―AC―B1的平面角,
由:OD1=OB1=B1D=2知--文科數(shù)學.files/image106.gif)
解法二:由ABCD―A1B1C1D1為四棱柱,得面BB1D1D⊥面ABCD
所以O(shè)1D1在平面ABCD上的射影為BD,由四邊形ABCD為正方形,AC⊥BD,由三垂線定理知,O1D1⊥AC。可得D1O1⊥平面AB1C。
又因為B1O⊥AC,所以∠D1OB1所求二面角D1―AC―B1的平面角,
--文科數(shù)學.files/image108.gif)
20.解:(1)曲線C上任意一點M到點F(0,1)的距離比它到直線--文科數(shù)學.files/image084.gif) 的距離小1,
的距離小1,
可得|MF|等于M到y(tǒng)=-1的距離,由拋物線的定義知,M點的軌跡為--文科數(shù)學.files/image111.gif)
(2)當直線--文科數(shù)學.files/image113.gif) 的斜率不存在時,它與曲線C只有一個交點,不合題意,
的斜率不存在時,它與曲線C只有一個交點,不合題意,
當直線m與x軸不垂直時,設(shè)直線m的方程為--文科數(shù)學.files/image115.gif)
代入--文科數(shù)學.files/image117.gif) ①
①
--文科數(shù)學.files/image119.gif) 恒成立,
恒成立,
設(shè)交點A,B的坐標分別為--文科數(shù)學.files/image121.gif)
∴直線m與曲線C恒有兩個不同交點。
則--文科數(shù)學.files/image123.gif) ②
② --文科數(shù)學.files/image125.gif) ③
③
--文科數(shù)學.files/image127.gif)
--文科數(shù)學.files/image129.gif)
故直線m的方程為--文科數(shù)學.files/image131.gif)
21.解:(1)由已知得--文科數(shù)學.files/image133.gif)
--文科數(shù)學.files/image135.gif)
(2)--文科數(shù)學.files/image137.gif)
--文科數(shù)學.files/image139.gif)
--文科數(shù)學.files/image141.gif)
(3)--文科數(shù)學.files/image143.gif)
--文科數(shù)學.files/image145.gif)

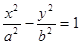 的左右兩支分別交于M,N兩點,與雙曲線C的右準線相交于P點,點F為右焦點,若
的左右兩支分別交于M,N兩點,與雙曲線C的右準線相交于P點,點F為右焦點,若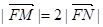 ,
,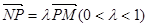 ,則實數(shù)
,則實數(shù)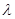 的值為 .
的值為 . 的左右兩支分別交于M,N兩點,與雙曲線C的右準線相交于P點,點F為右焦點,若
的左右兩支分別交于M,N兩點,與雙曲線C的右準線相交于P點,點F為右焦點,若 ,
, ,則實數(shù)
,則實數(shù) 的值為 .
的值為 .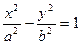 的左右兩支分別交于M,N兩點,與雙曲線C的右準線相交于P點,點F為右焦點,若
的左右兩支分別交于M,N兩點,與雙曲線C的右準線相交于P點,點F為右焦點,若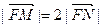 ,
,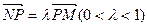 ,則實數(shù)
,則實數(shù)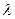 的值為 .
的值為 .