日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

已知曲線的參數(shù)方程是（是參數(shù)），以坐標(biāo)原點為極點，軸的正半軸為極軸建立極坐標(biāo)系，曲線:的極坐標(biāo)方程是=2，正方形ABCD的頂點都在上，且A,B,C,D依逆時針次序排列，點A的極坐標(biāo)為（2，）.

(Ⅰ)求點A,B,C,D的直角坐標(biāo)；

 (Ⅱ)設(shè)P為上任意一點，求的取值范圍.

【命題意圖】本題考查了參數(shù)方程與極坐標(biāo)，是容易題型.

【解析】(Ⅰ)由已知可得，，

，，

即A(1，)，B（－，1），C（―1，―），D（，－1），

(Ⅱ)設(shè)，令=，

則==，

∵，∴的取值范圍是[32,52]

已知，設(shè)和是方程的兩個根，不等式對任意實數(shù)恒成立；函數(shù)有兩個不同的零點.求使“P且Q”為真命題的實數(shù)的取值范圍.

【解析】本試題主要考查了命題和函數(shù)零點的運用。由題設(shè)x₁＋x₂＝a，x₁x₂＝－2，

∴|x₁－x₂|＝＝.

當(dāng)a∈[1,2]時，的最小值為3. 當(dāng)a∈[1,2]時，的最小值為3.

要使|m－5|≤|x₁－x₂|對任意實數(shù)a∈[1,2]恒成立，只須|m－5|≤3，即2≤m≤8.

由已知，得f(x)＝3x²＋2mx＋m＋＝0的判別式

Δ＝4m²－12(m＋)＝4m²－12m－16>0，

得m<－1或m>4.

可得到要使“P∧Q”為真命題，只需P真Q真即可。

解：由題設(shè)x₁＋x₂＝a，x₁x₂＝－2，

∴|x₁－x₂|＝＝.

當(dāng)a∈[1,2]時，的最小值為3.

要使|m－5|≤|x₁－x₂|對任意實數(shù)a∈[1,2]恒成立，只須|m－5|≤3，即2≤m≤8.

由已知，得f(x)＝3x²＋2mx＋m＋＝0的判別式

Δ＝4m²－12(m＋)＝4m²－12m－16>0，

得m<－1或m>4.

綜上，要使“P∧Q”為真命題，只需P真Q真，即

解得實數(shù)m的取值范圍是(4,8]

已知函數(shù)，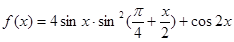

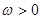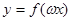(1)設(shè)常數(shù)，若在區(qū)間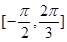上是增函數(shù)，求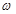的取值范圍；

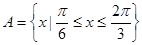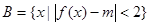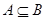(2)設(shè)集合，，若,求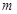的取值范圍.

【解析】本試題主要考查了三角函數(shù)的性質(zhì)的運用以及集合關(guān)系的運用。

第一問中利用

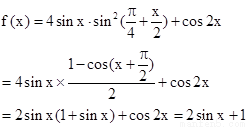
利用函數(shù)的單調(diào)性得到，參數(shù)的取值范圍。

第二問中，由于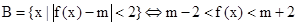解得參數(shù)m的取值范圍。

(1)由已知

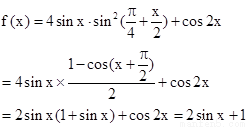
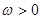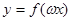又因為常數(shù)，若在區(qū)間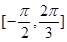上是增函數(shù)故參數(shù)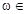 

 (2)因為集合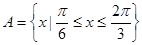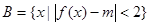，，若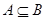

由已知得,,,

,,

,,,

所以函數(shù)f(x)的值以6為周期重復(fù)性出現(xiàn).,所以f（2009）= f（5）=1,故選C.

答案:C.

【命題立意】:本題考查歸納推理以及函數(shù)的周期性和對數(shù)的運算.

設(shè)函數(shù)f（x）=在[1，+∞上為增函數(shù).  

（1）求正實數(shù)a的取值范圍；

（2）比較的大小，說明理由；

（3）求證：（n∈N*, n≥2）

【解析】第一問中，利用

解:（1）由已知：，依題意得：≥0對x∈[1，+∞恒成立

∴ax－1≥0對x∈[1，+∞恒成立    ∴a－1≥0即：a≥1

（2）∵a=1   ∴由（1）知：f（x）=在[1，+∞)上為增函數(shù)，

∴n≥2時：f（）=

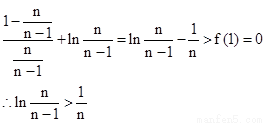
 (3)  ∵   ∴