
題目列表(包括答案和解析)
我國著名數學家華羅庚曾說過:撌?斃問鄙僦憊郟?紊偈?蹦訝胛ⅲ皇?謂岷習侔愫茫?衾敕旨彝蚴灤輸.數學中,數和形是兩個最主要的研究對象,它們之間有著十分密切的聯系,在一定條件下,數和形之間可以相互轉化,相互滲透.
數形結合的基本思想,就是在研究問題的過程中,注意把數和形結合起來考察,斟酌問題的具體情形,把圖形性質的問題轉化為數量關系的問題,或者把數量關系的問題轉化為圖形性質的問題,使復雜問題簡單化,抽象問題具體化,化難為易,獲得簡便易行的成功方案.
例如,求1+2+3+4+…+n的值,其中n是正整數.
對于這個求和問題,如果采用純代數的方法(首尾兩頭加),問題雖然可以解決,但在求和過程中,需對n的奇偶性進行討論.
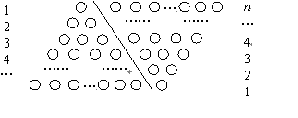
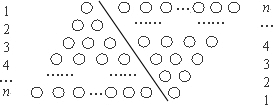
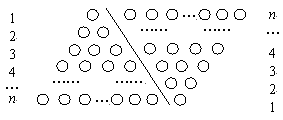
如果采用數形結合的方法,即用圖形的性質來說明數量關系的事實,那就非常的直觀.現利用圖形的性質來求1+2+3+4+…+n 的值,方案如下:如圖,斜線左邊的三角形圖案是由上到下每層依次分別為1,2,3,…,n個小圓圈排列組成的.而組成整個三角形小圓圈的個數恰為所求式子1+2+3+4+…+n的值.為求式子的值,現把左邊三角形倒放于斜線右邊,與原三角形組成一個平行四邊形.此時,組成平行四邊形的小圓圈共有n行,每行有(n+1)個小圓圈,所以組成平行四邊形小圓圈的總個數為n(n+1)個,因此,組成一個三角形小圓圈的個數為![]() ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=![]() .
.
(1
)仿照上述數形結合的思想方法,設計相關圖形,求1+3+5+7+…+(2n-1)的值,其中 n 是正整數.(要求:畫出圖形,并利用圖形做必要的推理說明)(2
)試設計另外一種圖形,求1+3+5+7+…+(2n-1)的值,其中n是正整數.(要求:畫出圖形,并利用圖形做必要的推理說明)| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n= .
.
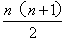 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n=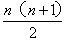 。
。
 ,即1+2+3+4+…+n=
,即1+2+3+4+…+n= .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com