
題目列表(包括答案和解析)
如圖,直線y= x+m與拋物線y=
x+m與拋物線y= x2-2x+l交于不同的兩點M、N(點M在點N的左側).
x2-2x+l交于不同的兩點M、N(點M在點N的左側).
(1)設拋物線的頂點為B,對稱軸l與直線y= x+m的交點為C,連結BM、BN,若S△MBC=
x+m的交點為C,連結BM、BN,若S△MBC= S△NBC,求直線MN的解析式;
S△NBC,求直線MN的解析式;
(2)在(1)條件下,已知點P(t,0)為x軸上的一個動點,
①若△PMN為直角三角形,求點P的坐標.
②若∠MPN>90°,則t的取值范圍是 .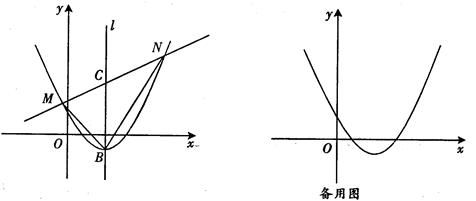
 x+m與拋物線y=
x+m與拋物線y= x2-2x+l交于不同的兩點M、N(點M在點N的左側).
x2-2x+l交于不同的兩點M、N(點M在點N的左側). x+m的交點為C,連結BM、BN,若S△MBC=
x+m的交點為C,連結BM、BN,若S△MBC= S△NBC,求直線MN的解析式;
S△NBC,求直線MN的解析式;
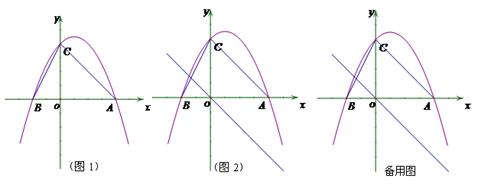
如圖1,二次函數y=ax2+bx+c(a≠0)的圖像與x軸交于點A、點B,與y軸交于點C,且A、B兩點的坐標分別是(4,0)、(0,-2),tan∠BCO=![]() (1)求拋物線解析式;(2)點M為拋物線上一點,若以MB為直徑的圓與直線BC相切于點B,求點M的坐標;(3) 如圖2,若點P是拋物線上的動點,點Q是直線y=-x的動點,是否存在以點P、Q、C、O為頂點且以OC為一邊的四邊形是直角梯形;如果存在,請求出點P的坐標,如果不存在,請說明理由.
(1)求拋物線解析式;(2)點M為拋物線上一點,若以MB為直徑的圓與直線BC相切于點B,求點M的坐標;(3) 如圖2,若點P是拋物線上的動點,點Q是直線y=-x的動點,是否存在以點P、Q、C、O為頂點且以OC為一邊的四邊形是直角梯形;如果存在,請求出點P的坐標,如果不存在,請說明理由.
【解析】(1)利用A、B兩點的坐標和tan∠BCO=![]() 求拋物線解析式
求拋物線解析式
(2)設點m(x,y),則由以MB為直徑的圓與直線BC相切于點B,說明了點B為直徑的一個端點,另外,BC直線方程為y=2x+4,利用BM的中點就是圓心坐標,BM垂直于CB,因此聯立方程組可得M的坐標
(3)假設存在以點P、Q、C、O為頂點且以OC為一邊的四邊形是直角梯形
則有幾種情況的一種直角為C,直角為P,直角為O,直角為Q的情況,那么分情況討論求解,利用一組對邊平行,一個角為直角,進行求解
如圖1,二次函數y=ax2+bx+c(a≠0)的圖像與x軸交于點A、點B,與y軸交于點C,且A、B兩點的坐標分別是(4,0)、(0,-2),tan∠BCO=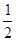 (1)求拋物線解析式;(2)點M為拋物線上一點,若以MB為直徑的圓與直線BC相切于點B,求點M的坐標;(3) 如圖2,若點P是拋物線上的動點,點Q是直線y=-x的動點,是否存在以點P、Q、C、O為頂點且以OC為一邊的四邊形是直角梯形;如果存在,請求出點P的坐標,如果不存在,請說明理由.
(1)求拋物線解析式;(2)點M為拋物線上一點,若以MB為直徑的圓與直線BC相切于點B,求點M的坐標;(3) 如圖2,若點P是拋物線上的動點,點Q是直線y=-x的動點,是否存在以點P、Q、C、O為頂點且以OC為一邊的四邊形是直角梯形;如果存在,請求出點P的坐標,如果不存在,請說明理由.
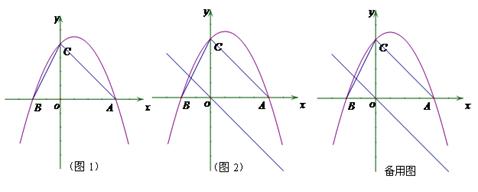
【解析】(1)利用A、B兩點的坐標和tan∠BCO=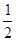 求拋物線解析式
求拋物線解析式
(2)設點m(x,y),則由以MB為直徑的圓與直線BC相切于點B,說明了點B為直徑的一個端點,另外,BC直線方程為y=2x+4,利用BM的中點就是圓心坐標,BM垂直于CB,因此聯立方程組可得M的坐標
(3)假設存在以點P、Q、C、O為頂點且以OC為一邊的四邊形是直角梯形
則有幾種情況的一種直角為C,直角為P,直角為O,直角為Q的情況 ,那么分情況討論求解,利用一組對邊平行,一個角為直角,進行求解
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com