
題目列表(包括答案和解析)
對于函數(shù)![]() ,如果存在實數(shù)
,如果存在實數(shù)![]() 使得
使得![]() ,那么稱
,那么稱![]() 為
為![]() 的生成函數(shù).
的生成函數(shù).
(1)下面給出兩組函數(shù),![]() 是否分別為
是否分別為![]() 的生成函數(shù)?并說明理由;
的生成函數(shù)?并說明理由;
第一組:![]() ;
;
第二組:![]() ;
;
(2)設(shè)![]() ,生成函數(shù)
,生成函數(shù)![]() .若不等式
.若不等式
![]() 在
在![]() 上有解,求實數(shù)
上有解,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() ,取
,取![]() ,生成函數(shù)
,生成函數(shù)![]() 圖像的最低點坐標(biāo)為
圖像的最低點坐標(biāo)為![]() .若對于任意正實數(shù)
.若對于任意正實數(shù)![]() 且
且![]() .試問是否存在最大的常數(shù)
.試問是否存在最大的常數(shù)![]() ,使
,使![]() 恒成立?如果存在,求出這個
恒成立?如果存在,求出這個![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
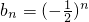 ,n∈N*,判斷{an}、{bn}是否為“p-擺動數(shù)列”,并說明理由;
,n∈N*,判斷{an}、{bn}是否為“p-擺動數(shù)列”,并說明理由;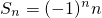 ,試問:數(shù)列{dn}是否為“p-擺動數(shù)列”,若是,求出p的取值范圍;若不是,說明理由.
,試問:數(shù)列{dn}是否為“p-擺動數(shù)列”,若是,求出p的取值范圍;若不是,說明理由. ,n∈N*,判斷{an}、{bn}是否為“p-擺動數(shù)列”,并說明理由;
,n∈N*,判斷{an}、{bn}是否為“p-擺動數(shù)列”,并說明理由;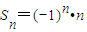 ,試問:數(shù)列{dn}是否為“p-擺動數(shù)列”,若是,求出p的取值范圍;若不是,說明理由.
,試問:數(shù)列{dn}是否為“p-擺動數(shù)列”,若是,求出p的取值范圍;若不是,說明理由.已知函數(shù) ,若存在
,若存在 使得
使得 恒成立,則稱
恒成立,則稱 是
是 的
的
一個“下界函數(shù)” .
(I)如果函數(shù) (t為實數(shù))為
(t為實數(shù))為 的一個“下界函數(shù)”,
的一個“下界函數(shù)”,
求t的取值范圍;
(II)設(shè)函數(shù) ,試問函數(shù)
,試問函數(shù) 是否存在零點,若存在,求出零點個數(shù);
是否存在零點,若存在,求出零點個數(shù);
若不存在,請說明理由.
已知函數(shù) ,若存在
,若存在 使得
使得 恒成立,則稱
恒成立,則稱 是
是 的
的
一個“下界函數(shù)” .
(I)如果函數(shù) (t為實數(shù))為
(t為實數(shù))為 的一個“下界函數(shù)”,
的一個“下界函數(shù)”,
求t的取值范圍;
(II)設(shè)函數(shù) ,試問函數(shù)
,試問函數(shù) 是否存在零點,若存在,求出零點個數(shù);
是否存在零點,若存在,求出零點個數(shù);
若不存在,請說明理由.
一、 填空題(48分)
1、4 2、(理)20(文)學(xué)%20文理科.files/image209.gif) 3、
3、學(xué)%20文理科.files/image211.gif) 4、
4、學(xué)%20文理科.files/image213.gif) 5、
5、學(xué)%20文理科.files/image215.gif) 6、
6、學(xué)%20文理科.files/image217.gif) 7、(理)
7、(理)學(xué)%20文理科.files/image219.gif) (文)4 8、6 9、
(文)4 8、6 9、學(xué)%20文理科.files/image221.gif) 10、
10、學(xué)%20文理科.files/image223.gif) 11、如
11、如學(xué)%20文理科.files/image225.gif) 12、
12、學(xué)%20文理科.files/image227.gif)
二、 選擇題(16分)
13、B 14、B 15、C 16、A
三、 解答題(86分)
17、(12分)(1)學(xué)%20文理科.files/image229.gif) ,則
,則學(xué)%20文理科.files/image231.gif) ……………………… (6分)
……………………… (6分)
(2)學(xué)%20文理科.files/image233.gif) ………………………………………(9分)
………………………………………(9分)
學(xué)%20文理科.files/image235.gif)
學(xué)%20文理科.files/image237.gif) …………………………………………………………(12分)
…………………………………………………………(12分)
18、(12分)(1)它是有一條側(cè)棱垂直于底面的四棱錐
學(xué)%20文理科.files/image239.gif)
…………………………………………………………(6分)
(注:評分注意實線、虛線;垂直關(guān)系;長度比例等)
(2)由題意,學(xué)%20文理科.files/image241.gif) ,則
,則學(xué)%20文理科.files/image243.gif) ,
,
學(xué)%20文理科.files/image245.gif) ,
,
∴需要3個這樣的幾何體可以拼成一個棱長為6的正方體學(xué)%20文理科.files/image133.gif) …(12分)
…(12分)
19、(14分)
(1)拋物線的焦點為(1,0) ……………………………………………………(2分)
設(shè)橢圓方程為學(xué)%20文理科.files/image247.gif) ,則
,則學(xué)%20文理科.files/image249.gif)
∴橢圓方程為學(xué)%20文理科.files/image251.gif) ……………………………………………(6分)
……………………………………………(6分)
(2)設(shè)學(xué)%20文理科.files/image253.gif) ,則
,則學(xué)%20文理科.files/image255.gif)
學(xué)%20文理科.files/image257.gif)
學(xué)%20文理科.files/image259.gif) ………………(8分)
………………(8分)
① 當(dāng)學(xué)%20文理科.files/image261.gif) 時,
時,學(xué)%20文理科.files/image263.gif) ,即
,即學(xué)%20文理科.files/image265.gif) 時,
時,學(xué)%20文理科.files/image267.gif) ;
;
② 當(dāng)學(xué)%20文理科.files/image269.gif) 時,
時,學(xué)%20文理科.files/image271.gif) ,即
,即學(xué)%20文理科.files/image273.gif) 時,
時,學(xué)%20文理科.files/image275.gif) ;
;
綜上,學(xué)%20文理科.files/image277.gif) 。……………………………………(14分)
。……………………………………(14分)
(注:也可設(shè)學(xué)%20文理科.files/image279.gif) 解答,參照以上解答相應(yīng)評分)
解答,參照以上解答相應(yīng)評分)
20、(14分)
(1)設(shè)當(dāng)天的旅游收入為L,由學(xué)%20文理科.files/image281.gif) 得
得
學(xué)%20文理科.files/image283.gif) ……………………………(2分)
……………………………(2分)
由學(xué)%20文理科.files/image285.gif) ,知
,知學(xué)%20文理科.files/image287.gif) …………………………………………(4分)
…………………………………………(4分)
學(xué)%20文理科.files/image289.gif) ,
,學(xué)%20文理科.files/image287.gif) 得
得學(xué)%20文理科.files/image291.gif) 。
。
即當(dāng)天的旅游收入是20萬到60萬。……………………………………………(7分)
(2)則每天的旅游收入上繳稅收后不低于220000元
由學(xué)%20文理科.files/image293.gif) (
(學(xué)%20文理科.files/image295.gif) )得
)得學(xué)%20文理科.files/image295.gif) ;
;
由學(xué)%20文理科.files/image297.gif) (
(學(xué)%20文理科.files/image299.gif) )得
)得學(xué)%20文理科.files/image301.gif) ;
;
∴學(xué)%20文理科.files/image303.gif) ………………………………………………………………………(11分)
………………………………………………………………………(11分)
代入可得學(xué)%20文理科.files/image305.gif) ∴
∴學(xué)%20文理科.files/image307.gif)
即每天游客應(yīng)不少于1540人。……………………………………………………(14分)
21、(16分)
(1) 由學(xué)%20文理科.files/image309.gif) ,得
,得學(xué)%20文理科.files/image311.gif) 則
則學(xué)%20文理科.files/image313.gif) 故
故學(xué)%20文理科.files/image315.gif) (4分)
(4分)
(2) 由學(xué)%20文理科.files/image177.gif) ,得
,得學(xué)%20文理科.files/image318.gif) 即
即學(xué)%20文理科.files/image320.gif)
∴學(xué)%20文理科.files/image322.gif) ,所以
,所以學(xué)%20文理科.files/image036.gif) 是不唯一的。……………………………………(10分)
是不唯一的。……………………………………(10分)
(3)學(xué)%20文理科.files/image325.gif) ,
,學(xué)%20文理科.files/image327.gif) ,
,學(xué)%20文理科.files/image329.gif) ;
;
∴學(xué)%20文理科.files/image331.gif) …………………………………………(12分)
…………………………………………(12分)
(文)………………………………………………………………………………(16分)
(理)一般地,對任意復(fù)數(shù)學(xué)%20文理科.files/image333.gif) ,有
,有學(xué)%20文理科.files/image335.gif) 。
。
證明:設(shè)學(xué)%20文理科.files/image337.gif) ,
,學(xué)%20文理科.files/image339.gif)
學(xué)%20文理科.files/image341.gif)
學(xué)%20文理科.files/image343.gif) ,
,學(xué)%20文理科.files/image345.gif)
學(xué)%20文理科.files/image347.gif)
∴學(xué)%20文理科.files/image335.gif) 。…………………………………………………(16分)
。…………………………………………………(16分)
22、(18分)
(1)學(xué)%20文理科.files/image349.gif) ………………………………………………………………(6分)
………………………………………………………………(6分)
(2)由學(xué)%20文理科.files/image351.gif) 解得
解得學(xué)%20文理科.files/image353.gif)
即學(xué)%20文理科.files/image355.gif)
解得學(xué)%20文理科.files/image357.gif) …………………………………(12分)
…………………………………(12分)
(3) 由學(xué)%20文理科.files/image359.gif) ,
,
又學(xué)%20文理科.files/image361.gif) ,
,
當(dāng)學(xué)%20文理科.files/image363.gif) 時,
時,學(xué)%20文理科.files/image196.gif) ,
,學(xué)%20文理科.files/image366.gif) ,
,
∴對于學(xué)%20文理科.files/image368.gif) 時,
時,學(xué)%20文理科.files/image370.gif) ,命題成立。………………(14分)
,命題成立。………………(14分)
以下用數(shù)學(xué)歸納法證明學(xué)%20文理科.files/image370.gif) 對
對學(xué)%20文理科.files/image203.gif) ,且
,且學(xué)%20文理科.files/image205.gif) 時,都有
時,都有學(xué)%20文理科.files/image207.gif) 成立
成立
假設(shè)學(xué)%20文理科.files/image372.gif) 時命題成立,即
時命題成立,即學(xué)%20文理科.files/image374.gif) ,
,
那么學(xué)%20文理科.files/image376.gif) 即
即學(xué)%20文理科.files/image378.gif) 時,命題也成立。
時,命題也成立。
∴存在滿足條件的區(qū)間學(xué)%20文理科.files/image370.gif) 。………………………………(18分)
。………………………………(18分)
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com