
題目列表(包括答案和解析)
設函數 的定義域為D,若存在非零實數h使得對于任意
的定義域為D,若存在非零實數h使得對于任意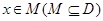 ,有
,有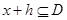 ,且
,且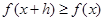 ,則稱
,則稱 為M上的“h階高調函數”。給出如下結論:
為M上的“h階高調函數”。給出如下結論:
①若函數 在R上單調遞增,則存在非零實數h使
在R上單調遞增,則存在非零實數h使 為R上的“h階高調函數”;
為R上的“h階高調函數”;
②若函數 為R上的“h階高調函數”,則
為R上的“h階高調函數”,則 在R上單調遞增;
在R上單調遞增;
③若函數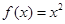 為區間
為區間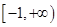 上的“h階高誣蔑財函數”,則
上的“h階高誣蔑財函數”,則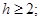
④若函數 在R上的奇函數,且
在R上的奇函數,且 時,
時,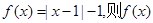 只能是R上的“4階高調函數”。
只能是R上的“4階高調函數”。
其中正確結論的序號為 ( )
A.①③ B.①④ C.②③ D.②④
已知函數 的圖象過坐標原點O,且在點
的圖象過坐標原點O,且在點 處的切線的斜率是
處的切線的斜率是 .
.
(Ⅰ)求實數 的值;
的值;
(Ⅱ)求 在區間
在區間 上的最大值;
上的最大值;
(Ⅲ)對任意給定的正實數 ,曲線
,曲線 上是否存在兩點P、Q,使得
上是否存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上?說明理由.
軸上?說明理由.
【解析】第一問當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
第二問當 時,
時, ,令
,令 得
得 ,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
,結合導數和函數之間的關系得到單調性的判定,得到極值和最值
第三問假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
(Ⅰ)當 時,
時, ,則
,則 。
。
依題意得: ,即
,即 解得
解得
(Ⅱ)由(Ⅰ)知,
①當 時,
時, ,令
,令 得
得
當 變化時,
變化時, 的變化情況如下表:
的變化情況如下表:
|
|
|
0 |
|
|
|
|
|
— |
0 |
+ |
0 |
— |
|
|
|
極小值 |
單調遞增 |
極大值 |
|
又 ,
, ,
, 。∴
。∴ 在
在 上的最大值為2.
上的最大值為2.
②當 時,
時,  .當
.當 時,
時,  ,
, 最大值為0;
最大值為0;
當 時,
時,  在
在 上單調遞增。∴
上單調遞增。∴ 在
在 最大值為
最大值為 。
。
綜上,當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為2;
上的最大值為2;
當 時,即
時,即 時,
時, 在區間
在區間 上的最大值為
上的最大值為 。
。
(Ⅲ)假設曲線 上存在兩點P、Q滿足題設要求,則點P、Q只能在
上存在兩點P、Q滿足題設要求,則點P、Q只能在 軸兩側。
軸兩側。
不妨設 ,則
,則 ,顯然
,顯然
∵ 是以O為直角頂點的直角三角形,∴
是以O為直角頂點的直角三角形,∴
即 (*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
(*)若方程(*)有解,存在滿足題設要求的兩點P、Q;
若方程(*)無解,不存在滿足題設要求的兩點P、Q.
若 ,則
,則 代入(*)式得:
代入(*)式得:
即 ,而此方程無解,因此
,而此方程無解,因此 。此時
。此時 ,
,
代入(*)式得:  即
即 (**)
(**)
令
 ,則
,則
∴ 在
在 上單調遞增, ∵
上單調遞增, ∵  ∴
∴ ,∴
,∴ 的取值范圍是
的取值范圍是 。
。
∴對于 ,方程(**)總有解,即方程(*)總有解。
,方程(**)總有解,即方程(*)總有解。
因此,對任意給定的正實數 ,曲線
,曲線 上存在兩點P、Q,使得
上存在兩點P、Q,使得 是以O為直角頂點的直角三角形,且此三角形斜邊中點在
是以O為直角頂點的直角三角形,且此三角形斜邊中點在 軸上
軸上
已知函數 在區間[0,1]上單調遞增,在區間[1,2]上單調遞減。
在區間[0,1]上單調遞增,在區間[1,2]上單調遞減。
(1)求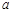 的值;
的值;
(2)若斜率為24的直線是曲線 的切線,求此直線方程;
的切線,求此直線方程;
(3)是否存在實數b,使得函數 的圖象與函數
的圖象與函數 的圖象恰有2個不同交點?若存在,求出實數b的值;若不存在,試說明理由.
的圖象恰有2個不同交點?若存在,求出實數b的值;若不存在,試說明理由.
已知函數 在區間
在區間 上為增函數,且
上為增函數,且 。
。
(1)當 時,求
時,求 的值;
的值;
(2)當 最小時,
最小時,
①求 的值;
的值;
②若 是
是 圖象上的兩點,且存在實數
圖象上的兩點,且存在實數 使得
使得
 ,證明:
,證明: 。
。
一、選擇題.(單項選擇,5×12=60分.答案涂在答題卡上的相應位置.)
1.C 2. A 3. B 4. B 5. B 6. B 7. A 8. C 9.D 10. B 11.D 12. B
二、填空題.( 5×4=20分,答案寫在答題紙的相應空格內.)
13..files/image249.gif) 14.②④⑤ 15.
14.②④⑤ 15..files/image251.gif) 16.11
16.11
三、解答題.(12×5+10=70分,答案寫在答題紙的答題區內.)
17.(Ⅰ)∵ m?n.files/image253.gif) ……… 2分
……… 2分
∴.files/image255.gif) ,解得
,解得.files/image257.gif) ……… 6分
……… 6分
(Ⅱ).files/image259.gif) ……… 8分
……… 8分
∵.files/image261.gif) ,∴
,∴.files/image263.gif) ………10分
………10分
∴.files/image265.gif) 的值域為[
的值域為[.files/image267.gif) ] ………12分
] ………12分
18.(Ⅰ)把一根長度為8的鐵絲截成3段,且三段的長度均為整數,共有21種解法.
(可視為8個相同的小球放入3個不同盒子,有.files/image269.gif) 種方法) … 3分
種方法) … 3分
其中能構成三角形的情況有3種情況:“2,3,
則所求的概率是.files/image271.gif) ……… 6分
……… 6分
(Ⅱ)根據題意知隨機變量.files/image273.gif) ……… 8分
……… 8分
∴.files/image275.gif) ……12分
……12分
19.(Ⅰ)∵點A、D分別是.files/image177.gif) 、
、.files/image179.gif) 的中點,∴
的中點,∴.files/image277.gif) . …… 2分
. …… 2分
∴∠.files/image279.gif) =90º.∴
=90º.∴.files/image281.gif) .∴
.∴ .files/image283.gif) ,
,
∵.files/image285.gif) ,∴
,∴.files/image195.gif) ⊥平面
⊥平面.files/image288.gif) . ……… 4分
. ……… 4分
∵.files/image290.gif) 平面
平面.files/image288.gif) ,∴
,∴.files/image293.gif) . ……… 5分
. ……… 5分
.files/image295.gif) (Ⅱ)建立如圖所示的空間直角坐標系
(Ⅱ)建立如圖所示的空間直角坐標系.files/image297.gif) .
.
則.files/image299.gif) (-1,0,0),
(-1,0,0),.files/image301.gif) (-2,1,0),
(-2,1,0),.files/image303.gif) (0,0,1).
(0,0,1).
∴.files/image305.gif) =(-1,1,0),
=(-1,1,0),.files/image307.gif) =(1,0,1), …6分
=(1,0,1), …6分
設平面.files/image309.gif) 的法向量為
的法向量為.files/image311.gif) =(x,y,z),則:
=(x,y,z),則:
.files/image313.gif) ,
……… 8分
,
……… 8分
令.files/image315.gif) ,得
,得.files/image317.gif) ,∴
,∴.files/image311.gif) =(1,1,-1)
=(1,1,-1)
顯然,.files/image319.gif) 是平面
是平面.files/image321.gif) 的一個法向量,
的一個法向量,.files/image319.gif) =(
=(.files/image324.gif)
.files/image326.gif) ). ………10分
). ………10分
∴cos<.files/image311.gif) ,
,.files/image319.gif) >=
>=.files/image329.gif) .
.
∴二面角.files/image198.gif) 的平面角的余弦值是
的平面角的余弦值是.files/image332.gif) .
………12分
.
………12分
20.(Ⅰ).files/image334.gif) ……… 4分
……… 4分
(Ⅱ)由橢圓的對稱性知:PRQS為菱形,原點O到各邊距離相等……… 5分
⑴當P在y軸上時,易知R在x軸上,此時PR方程為.files/image336.gif) ,
,
.files/image338.gif)
.files/image219.gif) . ……… 6分
. ……… 6分
⑵當P在x軸上時,易知R在y軸上,此時PR方程為.files/image336.gif) ,
,
.files/image338.gif)
.files/image219.gif) . ……… 7分
. ……… 7分
⑶當P不在坐標軸上時,設PQ斜率為k,.files/image340.gif) 、
、.files/image342.gif)
P在橢圓上,.files/image344.gif) .......①;R在橢圓上,
.......①;R在橢圓上,.files/image346.gif) ....
....
②利用Rt△POR可得 .files/image348.gif) ……… 9分
……… 9分
即 .files/image350.gif)
整理得 .files/image352.gif) . ………11分
. ………11分
再將①②帶入,得.files/image219.gif)
綜上當.files/image217.gif) 時,有
時,有.files/image219.gif) . ………12分
. ………12分
21.(Ⅰ).files/image354.gif) 時,
時,.files/image356.gif) 單調遞減,
單調遞減,
當.files/image358.gif) 單調遞增。
單調遞增。
①若.files/image360.gif) 無解;
無解;
②若.files/image362.gif)
.files/image364.gif)
③若.files/image366.gif) 時,
時,.files/image368.gif) 上單調遞增,
上單調遞增,
.files/image370.gif) ;
;
所以.files/image372.gif) ……… 4分
……… 4分
(Ⅱ).files/image374.gif) 則
則.files/image376.gif)
設.files/image378.gif) 則
則.files/image380.gif) 時,
時,
.files/image382.gif) 單調遞減,
單調遞減,.files/image384.gif) 單調遞增,
單調遞增,
所以.files/image386.gif) 因為對一切
因為對一切.files/image388.gif)
恒成立,所以.files/image390.gif) ; ……… 8分
; ……… 8分
(Ⅲ)問題等價于證明.files/image392.gif) ,
,
由(Ⅰ)可知.files/image394.gif)
當且僅當.files/image396.gif) 時取到,設
時取到,設.files/image398.gif)
則.files/image400.gif) ,當且僅當
,當且僅當.files/image315.gif) 時取到,
時取到,
從而對一切.files/image403.gif) 成立. ………12分
成立. ………12分
22.(Ⅰ)連接OC,∵OA=OB,CA=CB ∴OC⊥AB∴AB是⊙O的切線 … 5分
(Ⅱ)∵ED是直徑,∴∠ECD=90°∴∠E+∠EDC=90°
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC,∴∠BCD=∠E
又∵∠CBD+∠EBC,∴△BCD∽△BEC ∴.files/image405.gif) ∴BC2=BD•BE
∴BC2=BD•BE
∵tan∠CED=.files/image071.gif) ,∴
,∴.files/image408.gif) ∵△BCD∽△BEC, ∴
∵△BCD∽△BEC, ∴.files/image410.gif)
設BD=x,則BC=2 又BC2=BD•BE,∴(2x)2=x•(x+6)
解得x1=0,x2=2, ∵BD>0, ∴BD=2∴OA=OB=BD+OD=3+2=5 … 10分
23.(Ⅰ).files/image412.gif) … 5分
… 5分
(Ⅱ).files/image414.gif) … 10分
… 10分
23.(Ⅰ).files/image416.gif) ,
,.files/image418.gif) … 5分
… 5分
(Ⅱ).files/image420.gif)
.files/image422.gif) … 10分
… 10分
本資料由《七彩教育網》www.7caiedu.cn 提供!
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com