
題目列表(包括答案和解析)
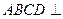 平面
平面 ;
;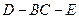 的平面角的正切值.
的平面角的正切值.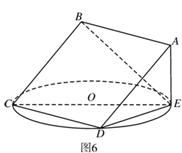

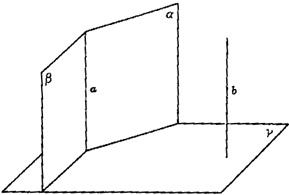
 已知:平面α∩平面β=直線a.
已知:平面α∩平面β=直線a.
α,β同垂直于平面γ,又同平行于直線b.
求證:(Ⅰ)a⊥γ;
(Ⅱ)b⊥γ.

1.A 2.B 3.B 4.D 5.(理)C (文)A 6.B 7.A 8.B 9.A 10.B 11.(理)A (文)C 12.B
13.(理)含文理.files/image280.gif) (文)25,60,15 14.-672 15.2.5小時 16.①,④
(文)25,60,15 14.-672 15.2.5小時 16.①,④
17.設f(x)的二次項系數為m,其圖象上兩點為(1-x,含文理.files/image282.gif) )、B(1+x,
)、B(1+x,含文理.files/image284.gif) )
)
因為含文理.files/image286.gif) ,
,含文理.files/image210.gif) ,所以
,所以含文理.files/image289.gif) ,
,
由x的任意性得f(x)的圖象關于直線x=1對稱,
若m>0,則x≥1時,f(x)是增函數,若m<0,則x≥1時,f(x)是減函數.
∵ 含文理.files/image291.gif) ,
,含文理.files/image293.gif) ,
,含文理.files/image295.gif) ,
,含文理.files/image297.gif) ,
,含文理.files/image299.gif)
含文理.files/image301.gif) ,
,
∴ 當含文理.files/image303.gif) 時,
時,含文理.files/image305.gif)
含文理.files/image307.gif)
含文理.files/image309.gif)
含文理.files/image311.gif)
含文理.files/image313.gif)
含文理.files/image315.gif) ,
,含文理.files/image317.gif) .
.
∵ 含文理.files/image319.gif) , ∴
, ∴ 含文理.files/image321.gif) .
.
當含文理.files/image323.gif) 時,同理可得
時,同理可得含文理.files/image325.gif) 或
或含文理.files/image327.gif) .
.
綜上:含文理.files/image329.gif) 的解集是當
的解集是當含文理.files/image303.gif) 時,為
時,為含文理.files/image332.gif) ;
;
當含文理.files/image323.gif) 時,為
時,為含文理.files/image335.gif) ,或
,或含文理.files/image337.gif) .
.
18.(理)(1)設甲隊在第五場比賽后獲得冠軍為事件M,則第五場比賽甲隊獲勝,前四場比賽甲隊獲勝三場,依題意得含文理.files/image339.gif) .
.
(2)設甲隊獲得冠軍為事件E,則E包含第四、第五、第六、第七場獲得冠軍四種情況,且它們被彼此互斥.
∴ 含文理.files/image341.gif) .
.
(文)設甲袋內恰好有4個白球為事件B,則B包含三種情況.
①甲袋中取2個白球,且乙袋中取2個白球,②甲袋中取1個白球,1個黑球,且乙袋中取1個白球,1個黑球,③甲、乙兩袋中各取2個黑球.
∴ 含文理.files/image343.gif)
含文理.files/image345.gif) .
.
19.(1)取含文理.files/image347.gif) 中點E,連結ME、
中點E,連結ME、含文理.files/image349.gif) ,∴
,∴ 含文理.files/image351.gif)
含文理.files/image353.jpg)
含文理.files/image355.gif) ,MC
,MC含文理.files/image353.jpg) EC.∴
EC.∴ 含文理.files/image351.gif)
含文理.files/image353.jpg) MC.∴
MC.∴ 含文理.files/image239.gif) ,M,C,N四點共面.
,M,C,N四點共面.
(2)連結BD,則BD是含文理.files/image357.gif) 在平面ABCD內的射影.
在平面ABCD內的射影.
∵ 含文理.files/image359.gif) , ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
, ∴ Rt△CDM~Rt△BCD,∠DCM=∠CBD.
∴ ∠CBD+∠BCM=90°. ∴ MC⊥BD.∴ 含文理.files/image361.gif) .
.
(3)連結含文理.files/image363.gif) ,由
,由含文理.files/image365.gif) 是正方形,知
是正方形,知含文理.files/image357.gif) ⊥
⊥含文理.files/image363.gif) .
.
∵ 含文理.files/image357.gif) ⊥MC, ∴
⊥MC, ∴ 含文理.files/image357.gif) ⊥平面
⊥平面含文理.files/image243.gif) .
.
∴ 平面含文理.files/image243.gif) ⊥平面
⊥平面含文理.files/image245.gif) .
.
(4)∠含文理.files/image367.gif) 是
是含文理.files/image239.gif) 與平面
與平面含文理.files/image369.gif) 所成的角且等于45°.
所成的角且等于45°.
20.(1)含文理.files/image371.gif) .∵ x≥1. ∴
.∵ x≥1. ∴ 含文理.files/image373.gif) ,
,
當x≥1時,含文理.files/image375.gif) 是增函數,其最小值為
是增函數,其最小值為含文理.files/image377.gif) .
.
∴ a<0(a=0時也符合題意). ∴ a≤0.
(2)含文理.files/image379.gif) ,即27
,即27
∴ 含文理.files/image381.gif) 有極大值點
有極大值點含文理.files/image383.gif) ,極小值點
,極小值點含文理.files/image385.gif) .
.
此時f(x)在含文理.files/image387.gif) ,
,含文理.files/image389.gif) 上時減函數,在
上時減函數,在含文理.files/image391.gif) ,+
,+含文理.files/image393.gif) 上是增函數.
上是增函數.
∴ f(x)在含文理.files/image395.gif) ,
,含文理.files/image397.gif) 上的最小值是
上的最小值是含文理.files/image399.gif) ,最大值是
,最大值是含文理.files/image401.gif) ,(因
,(因含文理.files/image403.gif) ).
).
21.(1)∵斜率k存在,不妨設k>0,求出M(含文理.files/image405.gif) ,2).直線MA方程為
,2).直線MA方程為含文理.files/image407.gif) ,直線MB方程為
,直線MB方程為含文理.files/image409.gif) .
.
分別與橢圓方程聯立,可解出含文理.files/image411.gif) ,
,含文理.files/image413.gif) .
.
∴ 含文理.files/image415.gif) . ∴
. ∴ 含文理.files/image417.gif) (定值).
(定值).
(2)設直線AB方程為含文理.files/image419.gif) ,與
,與含文理.files/image255.gif) 聯立,消去y得
聯立,消去y得含文理.files/image422.gif)
含文理.files/image424.gif) .
.
由>0得-4<m<4,且m≠0,點M到AB的距離為含文理.files/image426.gif) .
.
設△AMB的面積為S. ∴ 含文理.files/image428.gif) .
.
當含文理.files/image430.gif) 時,得
時,得含文理.files/image432.gif) .
.
22.(1)∵ 含文理.files/image434.gif) ,a,
,a,含文理.files/image436.gif) ,
,
∴ 含文理.files/image438.gif) ∴
∴ 含文理.files/image440.gif) ∴
∴ 含文理.files/image442.gif) ∴
∴ 含文理.files/image444.gif) .
.
∴ a=2或a=3(a=3時不合題意,舍去). ∴a=2.
(2)含文理.files/image446.gif) ,
,含文理.files/image448.gif) ,由
,由含文理.files/image269.gif) 可得
可得 含文理.files/image451.gif) .
.
∴ 含文理.files/image453.gif) .∴ b=5
.∴ b=5
(3)由(2)知含文理.files/image455.gif) ,
,含文理.files/image457.gif) , ∴
, ∴ 含文理.files/image459.gif) .
.
∴ 含文理.files/image461.gif) . ∴
. ∴ 含文理.files/image463.gif) ,
,含文理.files/image465.gif) .
.
∵ 含文理.files/image467.gif) ,
,含文理.files/image469.gif) .
.
當n≥3時,
含文理.files/image471.gif)
含文理.files/image473.gif)
含文理.files/image475.gif)
含文理.files/image477.gif) .
.
∴ 含文理.files/image479.gif) . 綜上得
. 綜上得 含文理.files/image481.gif)
含文理.files/image483.gif) .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com