
題目列表(包括答案和解析)
已知關于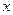 的不等式
的不等式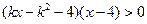 ,其中
,其中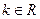 .
.
⑴當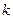 變化時,試求不等式的解集
變化時,試求不等式的解集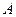 ;
;
⑵對于不等式的解集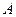 ,若滿足
,若滿足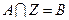 (其中
(其中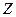 為整數集). 試探究集合
為整數集). 試探究集合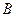 能否為有限集?若能,求出使得集合
能否為有限集?若能,求出使得集合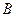 中元素個數最少的
中元素個數最少的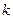 的所有取值,并用列舉法表示集合
的所有取值,并用列舉法表示集合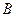 ;若不能,請說明理由.
;若不能,請說明理由.
已知關于 的不等式
的不等式 ,其中
,其中 .
.
⑴當 變化時,試求不等式的解集
變化時,試求不等式的解集 ;
;
⑵對于不等式的解集 ,若滿足
,若滿足 (其中
(其中 為整數集). 試探究集合
為整數集). 試探究集合 能否為有限集?若能,求出使得集合
能否為有限集?若能,求出使得集合 中元素個數最少的
中元素個數最少的 的所有取值,并用列舉法表示集合
的所有取值,并用列舉法表示集合 ;若不能,請說明理由.
;若不能,請說明理由.
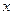 的不等式
的不等式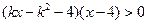 ,其中
,其中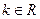 .
.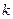 變化時,試求不等式的解集
變化時,試求不等式的解集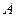 ;
;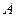 ,若滿足
,若滿足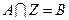 (其中
(其中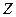 為整數集). 試探究集合
為整數集). 試探究集合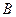 能否為有限集?若能,求出使得集合
能否為有限集?若能,求出使得集合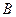 中元素個數最少的
中元素個數最少的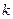 的所有取值,并用列舉法表示集合
的所有取值,并用列舉法表示集合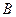 ;若不能,請說明理由.
;若不能,請說明理由. (12分)已知關于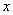 的不等式
的不等式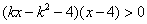 ,其中
,其中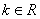 .
.
(1)當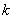 變化時,試求不等式的解集
變化時,試求不等式的解集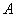 ;
;
(2)對于不等式的解集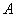 ,若滿足
,若滿足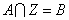 (其中
(其中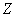 為整數集).
試探究集合
為整數集).
試探究集合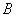 能否為有限集?若能,求出使得集合
能否為有限集?若能,求出使得集合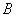 中元素個數最少的
中元素個數最少的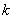 的所有取值,并用列舉法表示集合
的所有取值,并用列舉法表示集合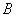 ;若不能,請說明理由.
;若不能,請說明理由.
(本題12分)已知關于 的不等式
的不等式 ,其中
,其中 .
.
(Ⅰ)當 變化時,試求不等式的解集
變化時,試求不等式的解集 ;
;
(Ⅱ)對于不等式的解集 ,若滿足
,若滿足 (其中
(其中 為整數集). 試探究集合
為整數集). 試探究集合 能否為有限集?若能,求出使得集合
能否為有限集?若能,求出使得集合 中元素個數最少的
中元素個數最少的 的所有取值,并用列舉法表示集合
的所有取值,并用列舉法表示集合 ;若不能,請說明理由.
;若不能,請說明理由.
一、填空題:(5’×11=55’)
題號
1
2
3
4
5
6
答案
.files/image195.gif)
.files/image197.gif)
0
(1,2)
2
.files/image199.gif)
題號
7
8
9
10
11
答案
.files/image201.gif)
4
8.3
.files/image203.gif)
②、③
二、選擇題:(4’×4=16’)
題號
12
13
14
|