
題目列表(包括答案和解析)
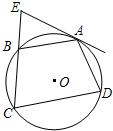 A.如圖,四邊形ABCD內接于⊙O,弧AB=弧AD,過A點的切線交CB的延長線于E點.
A.如圖,四邊形ABCD內接于⊙O,弧AB=弧AD,過A點的切線交CB的延長線于E點.
|
| 2 |
| π |
| 4 |
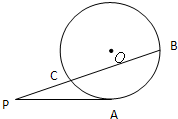
 A.如圖,⊙O的直徑AB的延長線與弦CD的延長線相交于點P,E為⊙O上一點,AE=AC,DE交AB于點F.求證:△PDF∽△POC.
A.如圖,⊙O的直徑AB的延長線與弦CD的延長線相交于點P,E為⊙O上一點,AE=AC,DE交AB于點F.求證:△PDF∽△POC.
|
|
| π |
| 4 |
| 2 |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
 A.(極坐標系與參數方程選做題) 已知圓ρ=3cosθ,則圓截直線
A.(極坐標系與參數方程選做題) 已知圓ρ=3cosθ,則圓截直線
|
| 3 |
| ax2+1 |
| bx+c |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
A.(幾何證明選講選做題)
如圖,已知AB為圓O的直徑,BC切圓O于點B,AC交圓O于點P,E為線段BC的中點.求證:OP⊥PE.

B.(矩陣與變換選做題)
已知M= ,N=
,N= ,設曲線y=sinx在矩陣MN對應的變換作用下得到曲線F,求F的方程.
,設曲線y=sinx在矩陣MN對應的變換作用下得到曲線F,求F的方程.
C.(坐標系與參數方程選做題)
在平面直角坐標系xOy中,直線m的參數方程為 (t為參數);在以O為極點、射線Ox為極軸的極坐標系中,曲線C的極坐標方程為ρsinθ=8cosθ.若直線m與曲線C交于A、B兩點,求線段AB的長.
(t為參數);在以O為極點、射線Ox為極軸的極坐標系中,曲線C的極坐標方程為ρsinθ=8cosθ.若直線m與曲線C交于A、B兩點,求線段AB的長.
D.(不等式選做題)
設x,y均為正數,且x>y,求證:2x+ ≥2y+3.
≥2y+3.
一、填空題:(5’×11=55’)
題號
1
2
3
4
5
6
答案
.files/image195.gif)
.files/image197.gif)
0
(1,2)
2
.files/image199.gif)
題號
7
8
9
10
11
答案
.files/image201.gif)
4
8.3
.files/image203.gif)
②、③
二、選擇題:(4’×4=16’)
題號
12
13
14
|