
�}Ŀ�б�(�����𰸺ͽ���)
���タ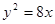 �Ľ��c(di��n)����(bi��o)�� ��
�Ľ��c(di��n)����(bi��o)�� ��
���タ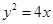 �Ľ��c(di��n)����(bi��o)�� ��
�Ľ��c(di��n)����(bi��o)�� ��
���タ �Ľ��c(di��n)����(bi��o)�� ��
�Ľ��c(di��n)����(bi��o)�� ��
���タ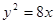 �Ľ��c(di��n)����(bi��o)�� ��
�Ľ��c(di��n)����(bi��o)�� ��
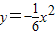 �Ľ��c(di��n)����(bi��o)�� ��
�Ľ��c(di��n)����(bi��o)�� ��һ������}����5����11��55����
�}̖
1
2
3
4
5
6
��
2008�W(xu��)��ȸ�����һ�W(xu��)���|(zh��)���{(di��o)�Мyԇ(��(sh��)�W(xu��)��).files/image195.gif)
2008�W(xu��)��ȸ�����һ�W(xu��)���|(zh��)���{(di��o)�Мyԇ(��(sh��)�W(xu��)��).files/image197.gif)
0
(1,2)
2
2008�W(xu��)��ȸ�����һ�W(xu��)���|(zh��)���{(di��o)�Мyԇ(��(sh��)�W(xu��)��).files/image199.gif)
�}̖
7
8
9
10
11
��
2008�W(xu��)��ȸ�����һ�W(xu��)���|(zh��)���{(di��o)�Мyԇ(��(sh��)�W(xu��)��).files/image201.gif)
4
8��3
2008�W(xu��)��ȸ�����һ�W(xu��)���|(zh��)���{(di��o)�Мyԇ(��(sh��)�W(xu��)��).files/image203.gif)
�ڡ���
�����x���}����4����4��16����
�}̖
12
13
14
|