
題目列表(包括答案和解析)
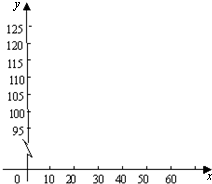
| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
 出結果)
出結果)
| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
 出結果)
出結果)| x | 10 | 20 | 30 | 40 | … |
| y | 95 | 100 | 105 | 110 | … |
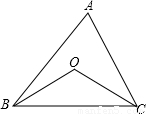
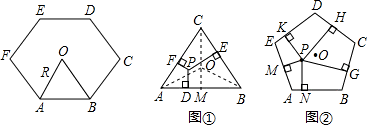 同學們已經認識了很多正多邊形,現以正六邊形為例再介紹與正多邊形相關的幾個概念.如正六邊形ABCDEF各邊對稱軸的交點O,又稱正六邊形的中心,其中OA稱正六邊形的半徑,通常用R表示,∠AOB稱為中心角,顯然.提出問題:正多邊形內任意一點到各邊距離之和與這個正多邊形的半徑R和中心角有什么關系?
同學們已經認識了很多正多邊形,現以正六邊形為例再介紹與正多邊形相關的幾個概念.如正六邊形ABCDEF各邊對稱軸的交點O,又稱正六邊形的中心,其中OA稱正六邊形的半徑,通常用R表示,∠AOB稱為中心角,顯然.提出問題:正多邊形內任意一點到各邊距離之和與這個正多邊形的半徑R和中心角有什么關系? a(h1+h2+h3)
a(h1+h2+h3) ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°, ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60° AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60° a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60° ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60° a(h1+h2+h3)
a(h1+h2+h3) ∠AOB=Rcos
∠AOB=Rcos ×120°=Rcos60°,
×120°=Rcos60°, ∠AOB=Rsin
∠AOB=Rsin ×120°=Rcos60°
×120°=Rcos60° AB×OM=
AB×OM= ×2Rsin60°•Rcos60°=R2sin60°cos60°
×2Rsin60°•Rcos60°=R2sin60°cos60° a(h1+h2+h3)=3R2sin60°cos60°
a(h1+h2+h3)=3R2sin60°cos60° ×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
×2Rsin60°(h1+h2+h3)=3R2sin60°cos60°
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com