
題目列表(包括答案和解析)
 在平面直角坐標系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4
在平面直角坐標系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4| 3 |
如圖1,在△ABC中,點P為BC邊中點,直線a繞頂點A旋轉(zhuǎn),若點B,P在直線a的異側(cè),BM⊥直線a于點M.CN⊥直線a于點N,連接PM,PN.
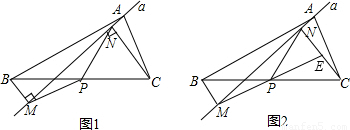
(1)延長MP交CN于點E(如圖2).
①求證:△BPM≌△CPE;
②求證:PM=PN;
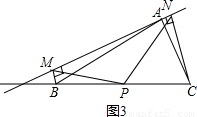
(2)若直線a繞點A旋轉(zhuǎn)到圖3的位置時,點B,P在直線a的同側(cè),其它條件不變,此時PM=PN還成立嗎?若成立,請給予證明;若不成立,請說明理由;
(3)若直線a繞點A旋轉(zhuǎn)到與BC邊平行的位置時,其它條件不變,請直接判斷四邊形MBCN的形狀及此時PM=PN還成立嗎?不必說明理由.
求證:①∠BAD=∠CAG;
②AC·AD=AE·AF.
(2)在問題(1)中,當(dāng)直線l向上平行移動,與⊙O相切時,其他條件不變.
①請你畫出變化后的圖形,并對照圖2-28標記字母;②問題(1)中的兩個結(jié)論是否成立?如果成立,請證明;如果不成立,請說明理由.

圖2-28
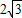 ,求直線l的方程;
,求直線l的方程;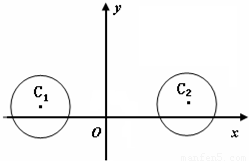
 ,求直線l的方程;
,求直線l的方程;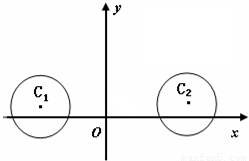
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com