
題目列表(包括答案和解析)
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 14 | 4 | 6 |
| 第三行 | 18 | 9 | 8 |
已知 是公差為d的等差數列,
是公差為d的等差數列, 是公比為q的等比數列
是公比為q的等比數列
(Ⅰ)若  ,是否存在
,是否存在 ,有
,有 ?請說明理由;
?請說明理由;
(Ⅱ)若 (a、q為常數,且aq
(a、q為常數,且aq 0)對任意m存在k,有
0)對任意m存在k,有 ,試求a、q滿足的充要條件;
,試求a、q滿足的充要條件;
(Ⅲ)若 試確定所有的p,使數列
試確定所有的p,使數列 中存在某個連續p項的和式數列中
中存在某個連續p項的和式數列中 的一項,請證明.
的一項,請證明.
【解析】第一問中,由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 為整數
為整數 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)中當 時,則
時,則
 即
即 ,其中
,其中 是大于等于
是大于等于 的整數
的整數
反之當 時,其中
時,其中 是大于等于
是大于等于 的整數,則
的整數,則 ,
,
顯然 ,其中
,其中

 、
、 滿足的充要條件是
滿足的充要條件是 ,其中
,其中 是大于等于
是大于等于 的整數
的整數
(3)中設 當
當 為偶數時,
為偶數時, 式左邊為偶數,右邊為奇數,
式左邊為偶數,右邊為奇數,
當 為偶數時,
為偶數時, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
當 時,符合題意。當
時,符合題意。當 ,
, 為奇數時,
為奇數時,
結合二項式定理得到結論。
解(1)由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 為整數
為整數 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)當 時,則
時,則
 即
即 ,其中
,其中 是大于等于
是大于等于 的整數反之當
的整數反之當 時,其中
時,其中 是大于等于
是大于等于 的整數,則
的整數,則 ,
,
顯然 ,其中
,其中

 、
、 滿足的充要條件是
滿足的充要條件是 ,其中
,其中 是大于等于
是大于等于 的整數
的整數
(3)設 當
當 為偶數時,
為偶數時, 式左邊為偶數,右邊為奇數,
式左邊為偶數,右邊為奇數,
當 為偶數時,
為偶數時, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
當 時,符合題意。當
時,符合題意。當 ,
, 為奇數時,
為奇數時,

 由
由 ,得
,得

 當
當 為奇數時,此時,一定有
為奇數時,此時,一定有 和
和 使上式一定成立。
使上式一定成立。 當
當 為奇數時,命題都成立
為奇數時,命題都成立
如果一個實數數列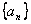 滿足條件:
滿足條件: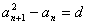 (
(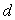 為常數,
為常數,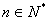 ),則稱這一數列
“偽等差數列”,
),則稱這一數列
“偽等差數列”, 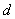 稱為“偽公差”。給出下列關于某個偽等差數列
稱為“偽公差”。給出下列關于某個偽等差數列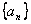 的結論:
的結論:
①對于任意的首項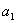 ,若
,若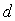 <0,則這一數列必為有窮數列;
<0,則這一數列必為有窮數列;
②當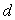 >0,
>0, 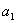 >0時,這一數列必為單調遞增數列;
>0時,這一數列必為單調遞增數列;
③這一數列可以是一個周期數列;
④若這一數列的首項為1,偽公差為3,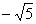 可以是這一數列中的一項;
可以是這一數列中的一項;
⑤若這一數列的首項為0,第三項為-1,則這一數列的偽公差可以是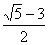 。
。
其中正確的結論是________________.
一支車隊有15輛車,某天依次出發執行運輸任務,第一輛車于下午2時出發,第二輛車于下午2時10分出發,第三輛車于下午2時20分出發,依此類推。假設所有的司機都連續開車,并都在下午6時停下來休息。
(1)到下午6時最后一輛車行駛了多長時間?
(2)如果每輛車的行駛速度都是60 ,這個車隊當天一共行駛了多少千米?
,這個車隊當天一共行駛了多少千米?
【解析】第一問中,利用第一輛車出發時間為下午2時,每隔10分鐘即 小時出發一輛
小時出發一輛
則第15輛車在 小時,最后一輛車出發時間為:
小時,最后一輛車出發時間為: 小時
小時
第15輛車行駛時間為: 小時(1時40分)
小時(1時40分)
第二問中,設每輛車行駛的時間為: ,由題意得到
,由題意得到
 是以
是以 為首項,
為首項, 為公差的等差數列
為公差的等差數列
則行駛的總時間為:
則行駛的總里程為: 運用等差數列求和得到。
運用等差數列求和得到。
解:(1)第一輛車出發時間為下午2時,每隔10分鐘即 小時出發一輛
小時出發一輛
則第15輛車在 小時,最后一輛車出發時間為:
小時,最后一輛車出發時間為: 小時
小時
第15輛車行駛時間為: 小時(1時40分)
……5分
小時(1時40分)
……5分
(2)設每輛車行駛的時間為: ,由題意得到
,由題意得到
 是以
是以 為首項,
為首項, 為公差的等差數列
為公差的等差數列
則行駛的總時間為: ……10分
……10分
則行駛的總里程為:
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 14 | 4 | 6 |
| 第三行 | 18 | 9 | 8 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com