
�}Ŀ�б�(�����𰸺ͽ���)
��֪m>1��ֱ�� ���E�AC��
���E�AC�� ��
�� ��
�� �քe��E�AC�����ҽ��c(di��n).
�քe��E�AC�����ҽ��c(di��n).
����(d��ng)ֱ���^�ҽ��c(di��n) �r(sh��)����ֱ���ķ���;
�r(sh��)����ֱ���ķ���;
�����O(sh��)ֱ���c�E�AC����A��B���c(di��n)����A
 ����B
����B
 �����ķքe��G��H.��ԭ�c(di��n)O���Ծ���GH��ֱ���ĈA��(n��i)����(sh��)��(sh��)m��ȡֵ����.[
�����ķքe��G��H.��ԭ�c(di��n)O���Ծ���GH��ֱ���ĈA��(n��i)����(sh��)��(sh��)m��ȡֵ����.[
����������һ������?y��n)�ֱ�� ��(j��ng)�^�c(di��n)
��(j��ng)�^�c(di��n) ��
�� ��0��������
��0�������� ��
�� ����
���� .����?y��n)�m>1������
.����?y��n)�m>1������ ����ֱ���ķ��̞�
����ֱ���ķ��̞�
�ڶ������O(sh��) ����
���� ����ȥx����
����ȥx���� ��
��
�t�� ��֪
��֪ <8,����
<8,����
���}��֪O��
 �����c(di��n).��
�����c(di��n).�� ��֪
��֪ �Ķ�
�Ķ� ���O(sh��)M��GH�����c(di��n)���tM��
���O(sh��)M��GH�����c(di��n)���tM�� ��.
��.
���}���֪��2|MO|<|GH|,�õ�����
��֪����(sh��)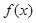 ���x��?y��n)�R����
���x��?y��n)�R����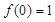 ����(du��)����
����(du��)����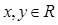 ����
����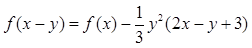 ��
��
��1����(sh��)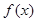 �ı��_(d��)ʽ��
�ı��_(d��)ʽ��
��2��������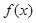 =
=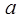 ������(g��)��(sh��)��(sh��)�⣬��(sh��)��(sh��)
������(g��)��(sh��)��(sh��)�⣬��(sh��)��(sh��)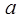 ��ȡֵ������
��ȡֵ������
����������һ���У�������?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131002338838152_ST.files/image002.png">����(du��)����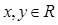 ����
����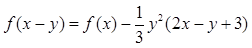 ��
��
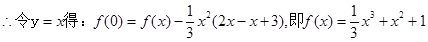
�ڶ����У���?y��n)鷽�?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131002338838152_ST.files/image001.png">=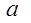 ������(g��)��(sh��)��(sh��)�⣬����
������(g��)��(sh��)��(sh��)�⣬����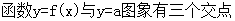
����?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131002338838152_ST.files/image010.png">��(d��ng)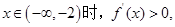
 ��
��
��(d��ng)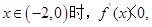
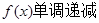 �Ķ��õ�������
�Ķ��õ�������
�⣺��1����?y��n)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131002338838152_ST.files/image002.png">����(du��)����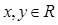 ����
����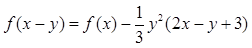 ��
��
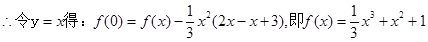
��2����?y��n)鷽�?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131002338838152_ST.files/image001.png">=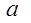 ������(g��)��(sh��)��(sh��)�⣬����
������(g��)��(sh��)��(sh��)�⣬����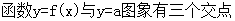
����?y��n)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012070911301664012899/SYS201207091131002338838152_ST.files/image010.png">����(d��ng)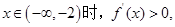
 ��
��
��(d��ng)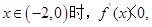
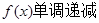 ����(d��ng)
����(d��ng)

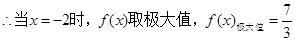 ��
��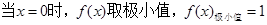
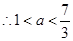
| 2 |
| 2 |
���������}����ɂ�(g��)����(sh��)��(sh��)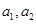 �M��
�M��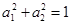 ����ô
����ô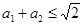 ����
����
�C�����£���(g��u)�캯��(sh��)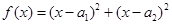 ����?y��n)�?du��)һ�Ќ�(sh��)��(sh��)
����?y��n)�?du��)һ�Ќ�(sh��)��(sh��)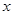 ������
������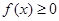 ��
��
��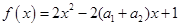 ���Ķ���
���Ķ���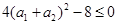 ������
������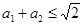 ��
��
����(j��)�����C����������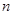 ��(g��)����(sh��)��(sh��)�M��
��(g��)����(sh��)��(sh��)�M��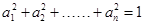 �r(sh��)������Ԙ�(g��u)�캯��(sh��)
�r(sh��)������Ԙ�(g��u)�캯��(sh��)
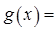 _______ ���M(j��n)һ���ܵõ��ĽY(ji��)Փ��
______________ �������C������
_______ ���M(j��n)һ���ܵõ��ĽY(ji��)Փ��
______________ �������C������
���������}����ɂ�(g��)����(sh��)��(sh��)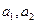 �M��
�M��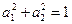 ����ô
����ô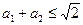 ����
����
�C�����£���(g��u)�캯��(sh��)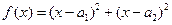 ����?y��n)�?du��)һ�Ќ�(sh��)��(sh��)
����?y��n)�?du��)һ�Ќ�(sh��)��(sh��) ������
������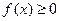 ��
��
��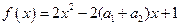 ���Ķ���
���Ķ���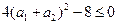 ������
������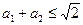 ��
��
����(j��)�����C����������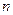 ��(g��)����(sh��)��(sh��)�M��
��(g��)����(sh��)��(sh��)�M��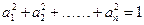 �r(sh��)������Ԙ�(g��u)�캯��(sh��)
�r(sh��)������Ԙ�(g��u)�캯��(sh��)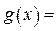 _______ ���M(j��n)һ���ܵõ��ĽY(ji��)Փ�� ______________ �������C������
_______ ���M(j��n)һ���ܵõ��ĽY(ji��)Փ�� ______________ �������C������
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com