
題目列表(包括答案和解析)
(2012新課標理)某花店每天以每枝![]() 元的價格從農場購進若干枝玫瑰花,然后以每枝
元的價格從農場購進若干枝玫瑰花,然后以每枝![]() 元的價格出售,
元的價格出售,
如果當天賣不完,剩下的玫瑰花作垃圾處理.
(1)若花店一天購進![]() 枝玫瑰花,求當天的利潤
枝玫瑰花,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]()
(單位:枝,![]() )的函數解析式.
)的函數解析式.
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
以100天記錄的各需求量的頻率作為各需求量發生的概率.
 (i)若花店一天購進
(i)若花店一天購進![]() 枝玫瑰花,
枝玫瑰花,![]() 表示當天的利潤(單位:元),求
表示當天的利潤(單位:元),求![]() 的分布列,
的分布列,
數學期望及方差;
(ii)若花店計劃一天購進16枝或17枝玫瑰花,你認為應購進16枝還是17枝?
請說明理由.
(本題滿分12分)
如圖6,在平面直角坐標系 中,設點
中,設點 ,直線
,直線 :
: ,點
,點 在直線
在直線 上移動,
上移動, 是線段
是線段 與
與 軸的交點,
軸的交點,  .
.
(I)求動點 的軌跡的方程
的軌跡的方程 ;
;
(II)設圓 過
過 ,且圓心
,且圓心 在曲線
在曲線 上,
上, 是圓
是圓 在
在 軸上截得的弦,當
軸上截得的弦,當 運動時弦長
運動時弦長 是否為定值?請說明理由.
是否為定值?請說明理由.
由于當前學生課業負擔較重,造成青少年視力普遍下降,現從某中學隨機抽取16名學生,經校醫用對數視力表檢査得到每個學生的視力狀況的莖葉圖(以小數點前的一位數字為莖,小數點后的一位數字為葉)如下:
(I )若視力測試結果不低于5 0,則稱為“好視力”,求校醫從這16人中隨機選取3人,至多有1人是“好視力”的概率;
(II)以這16人的樣本數據來估計整個學校的總體數據,若從該校(人數很多)任選3人,記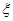 表示抽到“好視力”學生的人數,求
表示抽到“好視力”學生的人數,求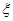 的分布列及數學期望,據此估計該校高中學生(共有5600人)好視力的人數
的分布列及數學期望,據此估計該校高中學生(共有5600人)好視力的人數

(本小題滿分12分)
如圖,在邊長為4的菱形 中,
中, .點
.點 分別在邊
分別在邊 上,點
上,點 與點
與點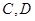 不重合,
不重合, ,
, .沿
.沿 將
將 翻折到
翻折到 的位置,使平面
的位置,使平面 ⊥平面
⊥平面 .
.

(1)求證: ⊥平面
⊥平面 ;
;
(2)當 取得最小值時,請解答以下問題:
取得最小值時,請解答以下問題:
(i)求四棱錐 的體積;
的體積;
(ii)若點 滿足
滿足 =
=
 (
( ),試探究:直線
),試探究:直線 與平面
與平面 所成角的大小是否一定大于
所成角的大小是否一定大于 ?并說明理由.
?并說明理由.
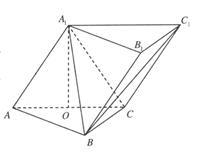
(本題滿分12分)如圖,在三棱柱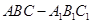 中,側面
中,側面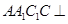 底面
底面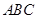 ,
,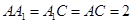 ,
,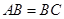 ,且
,且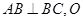 為
為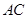 中點.
中點.
(I)證明: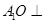 平面
平面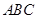 ;
;
(II)求直線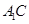 與平面
與平面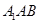 所成角的正弦值;
所成角的正弦值;
(III)在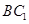 上是否存在一點
上是否存在一點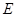 ,使得
,使得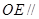 平面
平面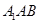 ,若不存在,說明理由;若存在,確定點
,若不存在,說明理由;若存在,確定點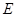 的位置.
的位置.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com