
題目列表(包括答案和解析)
解:能否投中,那得看拋物線與籃圈所在直線是否有交點。因為函數![]() 的零點是-2與4,籃圈所在直線x=5在4的右邊,拋物線又是開口向下的,所以投不中。
的零點是-2與4,籃圈所在直線x=5在4的右邊,拋物線又是開口向下的,所以投不中。
某城市出租汽車的起步價為10元,行駛路程不超出4km,則按10元的標準收租車費![]() 若行駛路程超出4km,則按每超出lkm加收2元計費(超出不足1km的部分按lkm計).從這個城市的民航機場到某賓館的路程為15km.某司機常駕車在機場與此賓館之間接送旅客,由于行車路線的不同以及途中停車時間要轉換成行車路程(這個城市規定,每停車5分鐘按lkm路程計費),這個司機一次接送旅客的行車路程ξ是一個隨機變量,
若行駛路程超出4km,則按每超出lkm加收2元計費(超出不足1km的部分按lkm計).從這個城市的民航機場到某賓館的路程為15km.某司機常駕車在機場與此賓館之間接送旅客,由于行車路線的不同以及途中停車時間要轉換成行車路程(這個城市規定,每停車5分鐘按lkm路程計費),這個司機一次接送旅客的行車路程ξ是一個隨機變量,
(1)他收旅客的租車費η是否也是一個隨機變量?如果是,找出租車費η與行車路程ξ的關系式;
(2)已知某旅客實付租車費38元,而出租汽車實際行駛了15km,問出租車在途中因故停車累計最多幾分鐘?這種情況下,停車累計時間是否也是一個隨機變量?
深夜,一輛出租車被牽涉進一起交通事故,該市有兩家出租車公司![]()
![]() 紅色出租車公司和藍色出租車公司,其中藍色出租車公司和紅色出租車公司分別占整個城市出租車的85%和15%.據現場目擊證明人說,事故現場的出租車是紅色,并對證人的辨別能力作了測試,測得他辨認的正確率為80%,于是警察就認定紅色出租車具有較大的肇事嫌疑.請問警察的認定對紅色出租車公平嗎?試說明理由.
紅色出租車公司和藍色出租車公司,其中藍色出租車公司和紅色出租車公司分別占整個城市出租車的85%和15%.據現場目擊證明人說,事故現場的出租車是紅色,并對證人的辨別能力作了測試,測得他辨認的正確率為80%,于是警察就認定紅色出租車具有較大的肇事嫌疑.請問警察的認定對紅色出租車公平嗎?試說明理由.
為了解高中一年級學生身高情況,某校按10%的比例對全校700名高中一年級學生按性別進行抽樣檢查,測得身高頻數分布表如下表1、表2.
表1:男生身高頻數分布表
|
身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
|
頻數 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生身高頻數分布表
|
身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
|
頻數 |
1 |
7 |
12 |
6 |
3 |
1 |
(I)求該校男生的人數并完成下面頻率分布直方圖;

(II)估計該校學生身高在 的概率;
的概率;
(III)從樣本中身高在180 190cm之間的男生中任選2人,求至少有1人身高在185
190cm之間的男生中任選2人,求至少有1人身高在185 190cm之間的概率。
190cm之間的概率。
【解析】第一問樣本中男生人數為40 ,
由分層抽樣比例為10%可得全校男生人數為400
(2)中由表1、表2知,樣本中身高在 的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在
的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在 的頻率
的頻率
故由 估計該校學生身高在
估計該校學生身高在 的概率
的概率
(3)中樣本中身高在180 185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185
185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185 190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖,故從樣本中身高在180
190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖,故從樣本中身高在180 190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185
190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185 190cm之間的可能結果數為9,因此,所求概率
190cm之間的可能結果數為9,因此,所求概率
由表1、表2知,樣本中身高在 的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在
的學生人數為:5+14+13+6+3+1=42,樣本容量為70 ,所以樣本中學生身高在
的頻率
 -----------------------------------------6分
-----------------------------------------6分
故由 估計該校學生身高在
估計該校學生身高在 的概率
的概率 .--------------------8分
.--------------------8分
(3)樣本中身高在180 185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185
185cm之間的男生有4人,設其編號為①②③④ 樣本中身高在185 190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖為:
190cm之間的男生有2人,設其編號為⑤⑥從上述6人中任取2人的樹狀圖為:

--10分
故從樣本中身高在180 190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185
190cm之間的男生中任選2人得所有可能結果數為15,求至少有1人身高在185 190cm之間的可能結果數為9,因此,所求概率
190cm之間的可能結果數為9,因此,所求概率
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 5 |
把函數 的圖象按向量
的圖象按向量 平移得到函數
平移得到函數 的圖象.
的圖象.
(1)求函數 的解析式; (2)若
的解析式; (2)若 ,證明:
,證明: .
.
【解析】本試題主要考查了函數 平抑變換和運用函數思想證明不等式。第一問中,利用設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 ,便可以得到結論。第二問中,令
,便可以得到結論。第二問中,令 ,然后求導,利用最小值大于零得到。
,然后求導,利用最小值大于零得到。
(1)解:設 上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入
上任意一點為(x,y)則平移前對應點是(x+1,y-2)代入 得y-2=ln(x+1)-2即y=ln(x+1),所以
得y-2=ln(x+1)-2即y=ln(x+1),所以 .……4分
.……4分
(2) 證明:令 ,……6分
,……6分
則 ……8分
……8分
 ,∴
,∴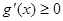 ,∴
,∴ 在
在 上單調遞增.……10分
上單調遞增.……10分
故 ,即
,即
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com