
題目列表(包括答案和解析)
 在平面直角坐標系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4
在平面直角坐標系xOy中,已知⊙C1:(x+3)2+(y-1)2=4和⊙C2:(x-5)2+(y-1)2=4| 3 |
 ,求直線l的方程;
,求直線l的方程;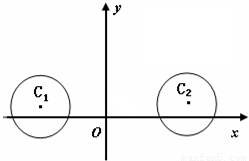
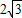 ,求直線l的方程;
,求直線l的方程;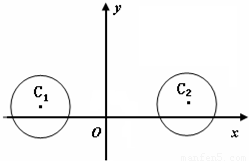
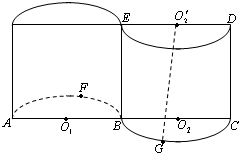 如圖所示的幾何體,是將高為2、底面半徑為1的圓柱沿過旋轉軸的平面切開后,將其中一半沿切面向右水平平移后形成的封閉體.
如圖所示的幾何體,是將高為2、底面半徑為1的圓柱沿過旋轉軸的平面切開后,將其中一半沿切面向右水平平移后形成的封閉體.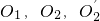 分別為AB,BC,DE的中點,F為弧AB的中點,G為弧BC的中點.
分別為AB,BC,DE的中點,F為弧AB的中點,G為弧BC的中點.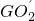 所成的角的大小(結果用反三角函數值表示).
所成的角的大小(結果用反三角函數值表示).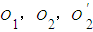 分別為AB,BC,DE的中點,F為弧AB的中點,G為弧BC的中點.
分別為AB,BC,DE的中點,F為弧AB的中點,G為弧BC的中點.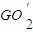 所成的角的大小(結果用反三角函數值表示).
所成的角的大小(結果用反三角函數值表示).
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com