日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

查看答案和解析>>

查看答案和解析>>

（本小題滿分12分）甲、乙兩人玩數字游戲，先由甲任想一個數字記為a，再由乙猜甲剛才想的數字，把乙想的數字記為b，且
（I）求兩人想的數字之差為3的概率；
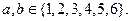
（II）若兩人想的數字相同或相差1，則稱“甲乙心有靈犀”，求“甲乙心有靈犀”的概率

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

一、選擇題：本大題共12小題，每小題5分，共60分.

1．A  2．C  3．C  4．A   5．C   6．C  7．B  8．C   9．D  10．D   11．D  12．D

二、填空題：本大題共4小題，每小題4分，共16分.

13．   14．    15．     16．40

三、解答題：本大題共6小題，共74分解答應寫出文字說明，證明過程或演算步驟.

17．解：

，聯合

得，即

當時，

當時，

∴當時，

當時，

18．解：由題意可知，這個幾何體是直三棱柱，且AC⊥BC，AC=BC=CC₁.

   （1）連結AC₁，AB₁.

    由直三棱柱的性質得AA₁⊥平面A₁B₁C₁，所以AA₁⊥A₁B₁，則四邊形ABB₁A₁為短形.

    由矩形性質得AB₁過A₁B的中點M.

在△AB₁C₁中，由中位線性質得MN//AC₁，

    又AC₁平面ACC₁A₁，MN平面ACC₁A₁，

所以MN//平面ACC₁A₁

   （2）因為BC⊥平面ACC₁A₁，AC平面ACC₁A₁，所以BC⊥AC₁.

在正方形ACC₁A₁中，A₁C⊥AC₁.

又因為BC∩A₁C=C，所以AC₁⊥平面A₁BC.

由MN//AC₁，得MN⊥平面A₁BC

19．解：（1）基本事件空間與點集中                                     

的元素一一對應． 

    因為S中點的總數為5×5=25(個)，所以基本事侉總數為n=25

    事件A包含的基本事件數共5個：

    (1，5)、(2，4)、(3，3)、(4，2)、(5，1)，

所以

   （2）B與C不是互斥事件．因為事件B與C可以同時發生，如甲贏一次，乙贏兩次的事件即符合題意

   （3）這種游戲規則不公平．由 (Ⅰ)知和為偶數的基本事件數為13個：

(1，1)、(1，3)、(1，5)、(2，2)、(2，4)、(3，1)、(3，3)、(3，5)、(4，2)、(4，4)、(5，1)、 (5，3)、(5，5)

所以甲贏的概率為，乙贏的概率為，

    所以這種游戲規則不公平．

20．（1）依題意，點的坐標為，可設，

直線的方程為，與聯立得

消去得．

由韋達定理得，．

于是．

，

   當，．

   （2）假設滿足條件的直線存在，其方程為，

設的中點為，與為直徑的圓相交于點，的中點為，

則，點的坐標為．

，

，

，

．

令，得，此時為定值，故滿足條件的直線存在，其方程為，即拋物線的通徑所在的直線．

21．解：（1）當時，，

∵，∴在上是減函數.

   （2）∵不等式恒成立，即不等式恒成立，

∴不等式恒成立. 當時，  不恒成立；

當時，不等式恒成立，即，∴.

當時，不等式不恒成立. 綜上，的取值范圍是.

22．解：（1）∵ 的橫坐標構成以為首項，為公差的等差數列

∴ .

∵ 位于函數的圖象上,

∴ ,

∴ 點的坐標為.

   （2）據題意可設拋物線的方程為：,

即．

∵ 拋物線過點（0，）,

∴ ,

∴   ∴ ．

∵ 過點且與拋物線只有一個交點的直線即為以為切點的切線，

∴ ．

∴ （），

∴

∴ ．

   （3）∵    ，

∴ 中的元素即為兩個等差數列與中的公共項，它們組成以為首項，以為公差的等差數列．

∵ ，且成等差數列，是中的最大數，

∴ ，其公差為．

當時，，

此時    ∴ 不滿足題意，舍去．

當時，，

此時，

∴ ．

當時，．

此時， 不滿足題意，舍去．

綜上所述，所求通項為．