
題目列表(包括答案和解析)
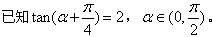
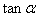 的值;
的值; 的值。
的值。 

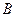







 的值;
的值; 的面積
的面積 ,求
,求 的值
的值 的值;
的值; ,是否存在一個實數
,是否存在一個實數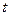 ,使數列
,使數列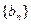 為等差數列?若存在,求出實數
為等差數列?若存在,求出實數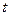 ;若不存在,請說明理由;
;若不存在,請說明理由; }的前n項和
}的前n項和
已知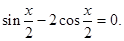
(Ⅰ)求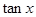 的值;
的值;
(Ⅱ)求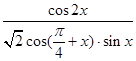 的值
的值
函數 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函數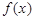 的最小正周期及其圖象的所有對稱軸的方程.
的最小正周期及其圖象的所有對稱軸的方程.
一.選擇題:DABBB ACACA
解析:1:由題干可得:

 故選
故選 .
.
2: 為拋物線
為拋物線 的內部(包括周界),
的內部(包括周界), 為動圓
為動圓 的內部(包括周界).該題的幾何意義是
的內部(包括周界).該題的幾何意義是 為何值時,動圓進入區域
為何值時,動圓進入區域 ,并被
,并被 所覆蓋.
所覆蓋.
 是動圓圓心的縱坐標,顯然結論應是
是動圓圓心的縱坐標,顯然結論應是 ,故可排除
,故可排除 ,而當
,而當 時,
時, (可驗證點
(可驗證點 到拋物線上點的最小距離為
到拋物線上點的最小距離為 ).故選
).故選 .
.
3:由f(x+2)=-f(x)得f(7.5)=-f(5.5)=f(3.5)=-f(1.5)=f(-0.5),由f(x)是奇函數,得f(-0.5)=-f(0.5)=-0.5,所以選B.
4:取a=100,b=10,此時P= ,Q=
,Q= =lg
=lg ,R=lg55=lg
,R=lg55=lg ,比較可知選P
,比較可知選P Q
Q R,所以選B
R,所以選B
5: f(x+ )=sin[
)=sin[ -2(x+
-2(x+ )]+sin[2(x+
)]+sin[2(x+ )]=-f(x),而f(x+π)=sin[
)]=-f(x),而f(x+π)=sin[ -2(x+π)]+sin[2(x+π)]=f(x).所以應選B;
-2(x+π)]+sin[2(x+π)]=f(x).所以應選B;
6:在同一直角坐標系中作出圓x +y
+y =4和直線4x+3y-12=0后,由圖可知距離最小的點在第一象限內,所以選A.
=4和直線4x+3y-12=0后,由圖可知距離最小的點在第一象限內,所以選A.
7:不等式的“極限”即方程,則只需驗證x=2,2.5, 和3哪個為方程
和3哪個為方程 的根,逐一代入,選C.
的根,逐一代入,選C.
8:當正n棱錐的頂點無限趨近于底面正多邊形中心時,則底面正多邊形便為極限狀態,此時棱錐相鄰兩側面所成二面角α→π,且小于π;當棱錐高無限大時,正n棱柱便又是另一極限狀態,此時α→ π,且大于
π,且大于 π,故選(A).
π,故選(A).
 9:取滿足題設的特殊函數f(x)=x,g(x)=|x|,則f(b)-f(-a)=a+b,g(a)-g(-b)=a-b,又f(a)-f(-b)=a+b,g(b)-g(-a)=b-a;∴選(C).
9:取滿足題設的特殊函數f(x)=x,g(x)=|x|,則f(b)-f(-a)=a+b,g(a)-g(-b)=a-b,又f(a)-f(-b)=a+b,g(b)-g(-a)=b-a;∴選(C).
10:作直線和圓的圖象,從圖中可以看出:
 的取值范圍應選(A).
的取值范圍應選(A).
二.填空題:11、 ;
12、
;
12、 ;
;
13、 ;
14、(x-1)2+(y-1)2=2;15、
;
14、(x-1)2+(y-1)2=2;15、 ;
;
解析:
 11:根據不等式解集的幾何意義,作函數
11:根據不等式解集的幾何意義,作函數 和
和
函數 的圖象(如圖),從圖上容易得出實數a的取
的圖象(如圖),從圖上容易得出實數a的取
值范圍是 。
。
12: 應用復數乘法的幾何意義,得

 ,
,
于是  故應填
故應填 
13:中獎號碼的排列方法是: 奇位數字上排不同的奇數有 種方法,偶位數字上排偶數的方法有
種方法,偶位數字上排偶數的方法有 ,從而中獎號碼共有
,從而中獎號碼共有 種,于是中獎面為
種,于是中獎面為
 故應填
故應填
14:解:由 得
得 =
= ,
,

 ,化簡得(x-1)2+(y-1)2=2
,化簡得(x-1)2+(y-1)2=2
15.解:依題意, =2,
=2,
 5,
5,
 =15,
=15,
 =
=
三.解答題:
16.解:(1)由 ,解之得
,解之得 ……………………5分
……………………5分
(2) …………………………9分
…………………………9分

 …………………………11分
…………………………11分
 …………………………12分
…………………………12分
17.解:(I) 的取值為1,3,又
的取值為1,3,又
|