
題目列表(包括答案和解析)
(文)某電信部門執行的新的電話收費標準中,其中本地網營業區內的通話費標準:前3分鐘為0.20元(不足3分鐘按3分鐘計算),以后的每分鐘收0.10元(不足1分鐘按1分鐘計算。)在一次實習作業中,某同學調查了A、B、C、D、E五人某天撥打的本地網營業區內的電話通話時間情況,其原始數據如下表所示:
|
|
A |
B |
C |
D |
E |
|
第一次通話時間 |
3分 |
3分45秒 |
3分55秒 |
3分20秒 |
6分 |
|
第二次通話時間 |
0分 |
4分 |
3分40秒 |
4分50秒 |
0分 |
|
第三次通話時間 |
0分 |
0分 |
5分 |
2分 |
0分 |
|
應繳話費(元) |
|
|
|
|
|
(1)在上表中填寫出各人應繳的話費;
(2)設通話時間為t分鐘,試根據上表完成下表的填寫(即這五人在這一天內的通話情況統計表):
|
時間段 |
頻數累計 |
頻數 |
頻率 |
累計頻率 |
|
0<t≤3 |
┯ |
2 |
0.2 |
0.2 |
|
3<t≤4 |
|
|
|
|
|
4<t≤5 |
|
|
|
|
|
5<t≤6 |
|
|
|
|
|
合計 |
正 正 |
|
|
|
(3)若該本地網營業區原來執行的電話收費標準是:每3分鐘為0.20元(不足3分鐘按3分鐘計算)。問這五人這天的實際平均通話費與原通話標準下算出的平均通話費相比,是增多了還是減少了?增或減了多少?
(文)某電信部門執行的新的電話收費標準中,其中本地網營業區內的通話費標準:前3分鐘為0.20元(不足3分鐘按3分鐘計算),以后的每分鐘收0.10元(不足1分鐘按1分鐘計算。)在一次實習作業中,某同學調查了A、B、C、D、E五人某天撥打的本地網營業區內的電話通話時間情況,其原始數據如下表所示:
| | A | B | C | D | E |
| 第一次通話時間 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通話時間 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通話時間 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 應繳話費(元) | | | | | |
| 時間段 | 頻數累計 | 頻數 | 頻率 | 累計頻率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | | | | |
| 4<t≤5 | | | | |
| 5<t≤6 | | | | |
| 合計 | 正 正 | | | |
| | A | B | C | D | E |
| 第一次通話時間 | 3分 | 3分45秒 | 3分55秒 | 3分20秒 | 6分 |
| 第二次通話時間 | 0分 | 4分 | 3分40秒 | 4分50秒 | 0分 |
| 第三次通話時間 | 0分 | 0分 | 5分 | 2分 | 0分 |
| 應繳話費(元) | | | | | |
| 時間段 | 頻數累計 | 頻數 | 頻率 | 累計頻率 |
| 0<t≤3 | ┯ | 2 | 0.2 | 0.2 |
| 3<t≤4 | | | | |
| 4<t≤5 | | | | |
| 5<t≤6 | | | | |
| 合計 | 正 正 | | | |
高二(3)班50名學生在一次百米測試中,成績全部介于13秒與19秒之間,將測試結果按如下方式分成六組:第一組,成績大于等于13秒且小于14秒;第二組,成績大于等于14秒且小于15秒;…;第六組,成績大于等于18秒且小于等于19秒.下圖是按上述分組方法得到的頻率分布直方圖.設成績小于17秒的學生人數占全班總人數的百分比為x, 成績大于等于15秒且小于17秒的學生人數為y,則從頻率分布直方圖中可分析出x和y分別為( ) 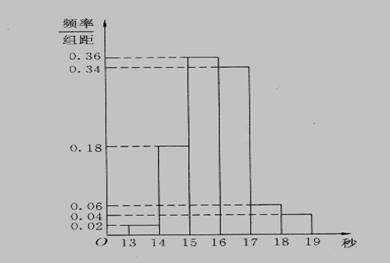
A.0.9,35 B. 0.1,45 C.0.1, 35 D. 0.9,45
高二(3)班50名學生在一次百米測試中,成績全部介于13秒與19秒之間,將測試結果按如下方式分成六組:第一組,成績大于等于13秒且小于14秒;第二組,成績大于等于14秒且小于15秒;…;第六組,成績大于等于18秒且小于等于19秒.下圖是按上述分組方法得到的頻率分布直方圖.設成績小于17秒的學生人數占全班總人數的百分比為x, 成績大于等于15秒且小于17秒的學生人數為y,則從頻率分布直方圖中可分析出x和y分別為( ) 
| A.0.9,35 | B.0.1,45 | C.0.1, 35 | D.0.9,45 |
一.選擇題:DABDA CDCBC
解析:1:由條件“函數是奇函數”可排除(B)、(C), 又 在區間
在區間 上不是單調遞減, 可淘汰(A),所以選(D).
上不是單調遞減, 可淘汰(A),所以選(D).
2:取滿足題設的特殊數值 a= ,
, ,
,
0> ,檢驗不等式(B),(C),(D)均不成立,選 (A).
,檢驗不等式(B),(C),(D)均不成立,選 (A).
3:由已知得

4:把x=1代入不等式組驗算得x=1是不等式組的解,則排除(B)、(C), 再把x=-3代入不等式組驗算得x=-3是不等式組的解,則排除(B),所以選(D).
5:本題學生很容易去分母得 ,然后解方程,不易實現目標。
,然后解方程,不易實現目標。
事實上,只要利用數形結合的思想,分別畫出 的圖象,容易發現在第一象限沒有交點。故選A。
的圖象,容易發現在第一象限沒有交點。故選A。
6:當m=0時,顯然有 ;若
;若 時,由
時,由 ,得
,得
 ,方程無解,m不存在。故選C。
,方程無解,m不存在。故選C。
7:由已知不妨設長 寬
寬 高
高 ,則對角線的長為
,則對角線的長為 .故選
.故選
8:由 得sin(x-
得sin(x- )>0,即2 kπ<x-
)>0,即2 kπ<x- <2kπ+π,取k=0即知選C.
<2kπ+π,取k=0即知選C.
9:用特值法:當n=2時,代入得C +C
+C =2,排除答案A、C;當n=4時,代入得C
=2,排除答案A、C;當n=4時,代入得C +C
+C +C
+C =8,排除答案D。所以選B。
=8,排除答案D。所以選B。
10:考慮由P0射到BC的中點上,這樣依次反射最終回到P0,此時容易求出tan =
= ,由題設條件知,1<x4<2,則tan
,由題設條件知,1<x4<2,則tan ≠
≠ ,排除A、B、D,故選C.
,排除A、B、D,故選C.
二.填空題:11、1;12、-1;13、23; 14、 ;15、
;15、 ;
;
解析:
11: 將已知方程變形為  ,
,
解這個一元二次方程,得

顯然有 , 而
, 而 ,于是
,于是
原式= =
= =
=
12: 由條件得 ,其中
,其中 .
.

 是已知函數的對稱軸,
是已知函數的對稱軸,
 , 即
, 即  ,
,
于是  故應填
故應填  .
.
13:因為正方體是對稱的幾何體,所以四邊形BFD1E在該正方體的面上的射影可分為:上下、左右、前后三個方向的射影,也就是在面ABCD、面ABB1A1、面ADD1A1上的射影.
四邊形BFD1E在面ABCD和面ABB1A1上的射影相同,如圖2所示;
四邊形BFD1E在該正方體對角面的ABC1D1內,它在面ADD1A1上的射影顯然是一條線段,如圖3所示. 故應填23.
14.(略)
15.解:由條件不難得 為等腰直角三角形,設圓的半徑為1,則
為等腰直角三角形,設圓的半徑為1,則 ,
, ,
,

 ,
,
 sin∠ACO=
sin∠ACO= )=
)=
三.解答題:
16.解:(1)將 ,
, 代入函數
代入函數 得
得 ,因為
,因為 ,所以
,所以 .
------------------2分
.
------------------2分
又因為 ,
, ,
, ,所以
,所以 ,
,
因此 .
------------------5分
.
------------------5分
(2)因為點 ,
, 是
是 的中點,
的中點, , 所以點
, 所以點 的坐標為
的坐標為 . ------------------7分
. ------------------7分
又因為點 在
在 的圖象上,
的圖象上,
所以 .------------------9分
.------------------9分
因為 ,所以
,所以 ,
,
從而得 或
或 .即
.即 或
或 ------------------12分
------------------12分
17.解:(Ⅰ)設“甲投球一次命中”為事件A,“乙投球一次命中”為事件B
由題意得  , 解得
, 解得 或
或 (舍去),
(舍去),
所以乙投球的命中率為 ------------------3分
------------------3分
(Ⅱ)由題設和(Ⅰ)知 -------------4分
-------------4分
 可能的取值為0,1,2,3,故
可能的取值為0,1,2,3,故 


 ,
, 
 的分布列為
的分布列為

0
1
2
3





 的數學期望
的數學期望 ------------------12分
------------------12分
18.解:(1)∵
 -------------------------------------------------1分
-------------------------------------------------1分
當 時,
時,
∴函數 在
在 上為增函數-----------------------------------------3分
上為增函數-----------------------------------------3分
∴ ,
, --------------------------4分
--------------------------4分
(2)證明:令
則
∵當 時
時 ,∴函數
,∴函數 在區間
在區間 上為減函數
上為減函數
∴
即在 上,
上,
∴在區間 上,函數
上,函數 的圖象在函數
的圖象在函數 的圖象的下方-----8分
的圖象的下方-----8分
(3)證明:∵
當 時,不等式顯然成立
時,不等式顯然成立
當 時
時
∵ =
= -----①
-----①

 -------------②-----10分
-------------②-----10分
①+②得

≥ (當且僅當
(當且僅當 時“=”成立)---------------13分
時“=”成立)---------------13分
∴當 時,不等式成立
時,不等式成立
綜上所述得 ≥
≥
 .--------------------------14分
.--------------------------14分
19.解:(Ⅰ)設 的坐標為
的坐標為 ,則
,則 且
且 .
.
解得 , 因此,點
, 因此,點  的坐標為
的坐標為 .
.
(Ⅱ) ,根據橢圓定義,
,根據橢圓定義,
得
 ,
,
 ,
, . ∴所求橢圓方程為
. ∴所求橢圓方程為 .
.
(Ⅲ) ,
, 橢圓的準線方程為
橢圓的準線方程為 .
.
設點 的坐標為
的坐標為
 ,
, 表示點
表示點 到
到 的距離,
的距離, 表示點
表示點 到橢圓的右準線的距離.
到橢圓的右準線的距離.
則 ,
, .
.
 , 令
, 令
 ,則
,則 ,
,
 當
當 ,
, ,
,  ,
, .
.
∴  在
在 時取得最小值.
時取得最小值.
因此, 最小值=
最小值= ,此時點
,此時點 的坐標為
的坐標為 -----------------14分
-----------------14分
20.解:(Ⅰ)取 中點
中點 ,連結
,連結 .
.
 為正三角形,
為正三角形, .
.
 在正三棱柱
在正三棱柱 中,平面
中,平面 平面
平面 ,
,  平面
平面 .
.
 取
取 中點
中點 ,以
,以 為原點,
為原點, ,
, ,
, 的方向為
的方向為 軸的正方向建立空間直角坐標系,則
軸的正方向建立空間直角坐標系,則 ,
, ,
, ,
, ,
,  ,
,
 ,
, ,
, .
.
 ,
, ,
,
 ,
, .
.
 平面
平面 .--------------------6分
.--------------------6分
(Ⅱ)設平面 的法向量為
的法向量為 .
.
 ,
, .
.  ,
, ,
,



令 得
得 為平面
為平面 的一個法向量.--------------------9分
的一個法向量.--------------------9分
由(Ⅰ)知 平面
平面 ,
,  為平面
為平面 的法向量.
的法向量.
 ,
, .
.
 二面角
二面角 的大小為
的大小為 . --------------------11分
. --------------------11分
(Ⅲ) 中,
中, ,
, .
.
在正三棱柱中, 到平面
到平面 的距離為
的距離為 .設點
.設點 到平面
到平面 的距離為
的距離為 .
.
由 得
得 ,
,  .
.
 點
點 到平面
到平面 的距離為
的距離為 --------------------14分
--------------------14分
21.解(1)∵不等式 ≤0的解集有且只有一個元素
≤0的解集有且只有一個元素
∴ 解得
解得 或
或 --------------------2分
--------------------2分
當 時函數
時函數 在
在 遞增,不滿足條件②--------------------3分
遞增,不滿足條件②--------------------3分
當 時函數
時函數 在(0,2)上遞減,滿足條件②--------------------4分
在(0,2)上遞減,滿足條件②--------------------4分
綜上得 ,即
,即 --------------------5分
--------------------5分
(2)由(1)知 , 當
, 當 時,
時,
當 ≥2時
≥2時 =
= =
= --------------------7分
--------------------7分
∴ --------------------8分
--------------------8分
(3)由題設可得 --------------------9分
--------------------9分
∵ ,
, ,
,
∴ ,
, 都滿足
都滿足 --------------------11分
--------------------11分
∵當 ≥3時,
≥3時,

即當 ≥3時,數列{
≥3時,數列{ }遞增,
}遞增,
∵
 ,由
,由
 ,可知
,可知 滿足
滿足 ----------------13分
----------------13分
∴數列{ }的變號數為3. ------------------14分
}的變號數為3. ------------------14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com