日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

(本題滿分16分)已知二次函數f (x) = x² ??ax + a (x∈R)同時滿足：①不等式 f (x) ≤ 0的解集有且只有一個元素；②在定義域內存在0 < x₁ < x₂，使得不等式f (x₁) > f (x₂)成立．設數列{a_n}的前 n 項和S_n = f (n)．（1）求函數f (x)的表達式；（2）求數列{a_n}的通項公式；（3）在各項均不為零的數列{c_n}中，若c_i·c_i+1 < 0，則稱c_i，c_i+1為這個數列{c_n}一對變號項．令c_n = 1 ?? （n為正整數），求數列{c_n}的變號項的對數．

（本小題滿分16分）設等差數列{a_n}的前n項和是S_n，已知S₃＝9，S₆＝36．
（1）求數列{a_n}的通項公式；
（2）是否存在正整數m、k，使a_m，a_m＋5，a_k成等比數列？若存在，求出m和k的值，若不存在，說明理由；
（3）設數列{b_n}的通項公式為b_n＝3n－2．集合A＝{x∣x＝a_n，n∈N^*}，B＝{x∣x＝b_n，n∈N^*}．將集合A∪B中的元素從小到大依次排列，構成數列c₁，c₂，c₃，…，求{c_n}的通項公式．

（本小題滿分16分）
已知數列﹛an﹜中，a2=p（p是不等于0的常數），Sn為數列﹛an﹜的前n項和，若對任意的正整數n都有Sn=.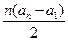
（1）證明：數列﹛an﹜為等差數列；
（2）記bn=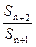+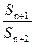，求數列﹛bn﹜的前n項和Tn；
（3）記cn=Tn-2n，是否存在正整數m，使得當n＞m時，恒有cn∈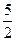（,3）？若存在，證明你的結論，并給出一個具體的m值；若不存在，請說明理由。

（本小題滿分16分）設等差數列{a_n}的前n項和是S_n，已知S₃＝9，S₆＝36．

（1）求數列{a_n}的通項公式；

（2）是否存在正整數m、k，使a_m，a_m＋5，a_k成等比數列？若存在，求出m和k的值，若不存在，說明理由；

（3）設數列{b_n}的通項公式為b_n＝3n－2．集合A＝{x∣x＝a_n，n∈N^*}，B＝{x∣x＝b_n，n∈N^*}．將集合A∪B中的元素從小到大依次排列，構成數列c₁，c₂，c₃，…，求{c_n}的通項公式．

（本小題滿分16分）

已知數列{a_n}的通項公式為a_n = (nÎN^*).

⑴求數列{a_n}的最大項；

⑵設b_n = ，試確定實常數p，使得{b_n}為等比數列；

⑶設，問：數列{a_n}中是否存在三項，，，使數列，，是等差數列？如果存在，求出這三項；如果不存在，說明理由.