
題目列表(包括答案和解析)
(本小題滿分12分)
甲、乙兩人下中國象棋,乙每局獲勝的概率為![]() .
.
若甲、乙比賽3局,求乙恰勝2局的概率.
若甲、乙比賽,甲每局獲勝的概率為![]() ,和局的概率為
,和局的概率為![]() .每局勝者得2分,負者得0分,和局則各得1分,規定積分先達到4分或4分以上者獲獎并終止比賽(若兩人同時達到4分,則兩人都不獲獎),求甲恰好在第3局比賽結束時獲獎的概率.
.每局勝者得2分,負者得0分,和局則各得1分,規定積分先達到4分或4分以上者獲獎并終止比賽(若兩人同時達到4分,則兩人都不獲獎),求甲恰好在第3局比賽結束時獲獎的概率.
已知點 (
( ),過點
),過點 作拋物線
作拋物線 的切線,切點分別為
的切線,切點分別為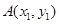 、
、 (其中
(其中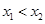 ).
).
(Ⅰ)若 ,求
,求 與
與 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,若以點 為圓心的圓
為圓心的圓 與直線
與直線 相切,求圓
相切,求圓 的方程;
的方程;
(Ⅲ)若直線 的方程是
的方程是 ,且以點
,且以點 為圓心的圓
為圓心的圓 與直線
與直線 相切,
相切,
求圓 面積的最小值.
面積的最小值.
【解析】本試題主要考查了拋物線的的方程以及性質的運用。直線與圓的位置關系的運用。
中∵直線 與曲線
與曲線 相切,且過點
相切,且過點 ,∴
,∴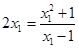 ,利用求根公式得到結論先求直線
,利用求根公式得到結論先求直線 的方程,再利用點P到直線的距離為半徑,從而得到圓的方程。
的方程,再利用點P到直線的距離為半徑,從而得到圓的方程。
(3)∵直線 的方程是
的方程是 ,
, ,且以點
,且以點 為圓心的圓
為圓心的圓 與直線
與直線 相切∴點
相切∴點 到直線
到直線 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即 ,借助于函數的性質圓
,借助于函數的性質圓 面積的最小值
面積的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直線 與曲線
與曲線 相切,且過點
相切,且過點 ,∴
,∴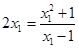 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵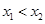 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,則
,則 的斜率
的斜率 ,
,
∴直線 的方程為:
的方程為: ,又
,又 ,
,
∴ ,即
,即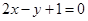 . -----------------7分
. -----------------7分
∵點 到直線
到直線 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即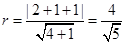 ,--------------8分
,--------------8分
故圓 的面積為
的面積為 . --------------------9分
. --------------------9分
(Ⅲ)∵直線 的方程是
的方程是 ,
, ,且以點
,且以點 為圓心的圓
為圓心的圓 與直線
與直線 相切∴點
相切∴點 到直線
到直線 的距離即為圓
的距離即為圓 的半徑,即
的半徑,即 , ………10分
, ………10分
∴
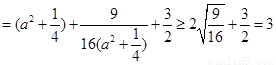 ,
,
當且僅當 ,即
,即 ,
, 時取等號.
時取等號.
故圓 面積的最小值
面積的最小值 .
.
| 日需求量x | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
某售報亭每天以每份0.4元的價格從報社購進若干份報紙,然后以每份1元的價格出售,如果當天賣不完,剩下的報紙以每份0.1元的價格賣給廢品收購站.
(Ⅰ)若售報亭一天購進270份報紙,求當天的利潤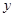 (單位:元)關于當天需求量
(單位:元)關于當天需求量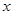 (單位:份,
(單位:份,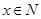 )的函數解析式.
)的函數解析式.
(Ⅱ)售報亭記錄了100天報紙的日需求量(單位:份),整理得下表:
|
日需求量 |
240 |
250 |
260 |
270 |
280 |
290 |
300 |
|
頻數 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
以100天記錄的需求量的頻率作為各銷售量發生的概率.
(1)若售報亭一天購進270份報紙, 表示當天的利潤(單位:元),求
表示當天的利潤(單位:元),求 的數學期望;
的數學期望;
(2)若售報亭計劃每天應購進270份或280份報紙,你認為購進270份報紙好,還是購進280份報紙好? 說明理由.
| 日需求量x | 240 | 250 | 260 | 270 | 280 | 290 | 300 |
| 頻數 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com