
題目列表(包括答案和解析)
(本小題滿分14分)在平面直角坐標系中,已知 為坐標原點,點
為坐標原點,點 的坐標為
的坐標為 ,點
,點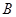 的坐標為
的坐標為 ,其中
,其中 且
且 .設
.設 .
.
(I)若 ,
, ,
, ,求方程
,求方程 在區間
在區間 內的解集;
內的解集;
(II)若點 是曲線
是曲線 上的動點.當
上的動點.當 時,設函數
時,設函數 的值域為集合
的值域為集合 ,不等式
,不等式 的解集為集合
的解集為集合 . 若
. 若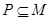 恒成立,求實數
恒成立,求實數 的最大值;
的最大值;
(III)根據本題條件我們可以知道,函數 的性質取決于變量
的性質取決于變量 、
、 和
和 的值. 當
的值. 當 時,試寫出一個條件,使得函數
時,試寫出一個條件,使得函數 滿足“圖像關于點
滿足“圖像關于點 對稱,且在
對稱,且在 處
處 取得最小值”.【說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.】
取得最小值”.【說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.】
 為坐標原點,點
為坐標原點,點 的坐標為
的坐標為 ,點
,點 的坐標為
的坐標為 ,其中
,其中 且
且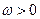 .設
.設 .
. ,
, ,
, ,求方程
,求方程 在區間
在區間 內的解集;
內的解集; 是曲線
是曲線 上的動點.當
上的動點.當 時,設函數
時,設函數 的值域為集合
的值域為集合 ,不等式
,不等式 的解集為集合
的解集為集合 . 若
. 若 恒成立,求實數
恒成立,求實數 的最大值;
的最大值; 的性質取決于變量
的性質取決于變量 、
、 和
和 的值. 當
的值. 當 時,試寫出一個條件,使得函數
時,試寫出一個條件,使得函數 滿足“圖像關于點
滿足“圖像關于點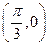 對稱,且在
對稱,且在 處
處 取得最小值”.【說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.】
取得最小值”.【說明:請寫出你的分析過程.本小題將根據你對問題探究的完整性和在研究過程中所體現的思維層次,給予不同的評分.】已知函數f(x)=ex-ax,其中a>0.
(1)若對一切x∈R,f(x)  1恒成立,求a的取值集合;
1恒成立,求a的取值集合;
(2)在函數f(x)的圖像上去定點A(x1, f(x1)),B(x2, f(x2))(x1<x2),記直線AB的斜率為k,證明:存在x0∈(x1,x2),使 恒成立.
恒成立.
【解析】解: 令
令 .
.
當 時
時 單調遞減;當
單調遞減;當 時
時 單調遞增,故當
單調遞增,故當 時,
時, 取最小值
取最小值
于是對一切 恒成立,當且僅當
恒成立,當且僅當 . ①
. ①
令 則
則
當 時,
時, 單調遞增;當
單調遞增;當 時,
時, 單調遞減.
單調遞減.
故當 時,
時, 取最大值
取最大值 .因此,當且僅當
.因此,當且僅當 時,①式成立.
時,①式成立.
綜上所述, 的取值集合為
的取值集合為 .
.
(Ⅱ)由題意知, 令
令 則
則


令 ,則
,則 .當
.當 時,
時, 單調遞減;當
單調遞減;當 時,
時, 單調遞增.故當
單調遞增.故當 ,
, 即
即
從而 ,
, 又
又

所以
 因為函數
因為函數 在區間
在區間 上的圖像是連續不斷的一條曲線,所以存在
上的圖像是連續不斷的一條曲線,所以存在 使
使 即
即 成立.
成立.
【點評】本題考查利用導函數研究函數單調性、最值、不等式恒成立問題等,考查運算能力,考查分類討論思想、函數與方程思想等數學方法.第一問利用導函數法求出 取最小值
取最小值 對一切x∈R,f(x)
對一切x∈R,f(x)  1恒成立轉化為
1恒成立轉化為 從而得出求a的取值集合;第二問在假設存在的情況下進行推理,然后把問題歸結為一個方程是否存在解的問題,通過構造函數,研究這個函數的性質進行分析判斷.
從而得出求a的取值集合;第二問在假設存在的情況下進行推理,然后把問題歸結為一個方程是否存在解的問題,通過構造函數,研究這個函數的性質進行分析判斷.
一、選擇題(每小題5分,共60分)
1.A 2.C 3.C 4.D 5.B 6.A 7.D 8.D 9.C 10.B 11.B 12.D
二、填空題(每小題4分,共16分)
13. 14.3825 15.1 16.0ⅠⅡ
14.3825 15.1 16.0ⅠⅡ
三、解答題
17.解:(Ⅰ)在 中,由
中,由 及余弦定理得
及余弦定理得
而 ,則
,則 ;
;
(Ⅱ)由 及正弦定理得
及正弦定理得 ,
,
而 ,則
,則
于是 ,
,
由 得
得 ,當
,當 即
即 時,
時, 。
。
18解:(Ⅰ)基本事件 共有36個,方程有正根等價于
共有36個,方程有正根等價于 ,即
,即 。設“方程有兩個正根”為事件
。設“方程有兩個正根”為事件 ,則事件
,則事件 包含的基本事件為
包含的基本事件為 共4個,故所求的概率為
共4個,故所求的概率為 ;
;
(Ⅱ)試驗的全部結果構成區域 ,其面積為
,其面積為
設“方程無實根”為事件 ,則構成事件
,則構成事件 的區域為
的區域為
 ,其面積為
,其面積為
故所求的概率為
19.解:(Ⅰ)證明:由 平面
平面 及
及 得
得 平面
平面 ,則
,則
而 平面
平面 ,則
,則 ,又
,又 ,則
,則 平面
平面 ,
,
又 平面
平面 ,故
,故 。
。
(Ⅱ)在 中,過點
中,過點 作
作 于點
于點 ,則
,則 平面
平面 .
.
由已知及(Ⅰ)得 .
.
故
(Ⅲ)在 中過點
中過點 作
作 交
交 于點
于點 ,在
,在 中過點
中過點 作
作 交
交 于點
于點 ,連接
,連接 ,則由
,則由 得
得
由平面 平面
平面 ,則
,則 平面
平面
再由 得
得 平面
平面 ,又
,又 平面
平面 ,則
,則 平面
平面 .
.
故當點 為線段
為線段 上靠近點
上靠近點 的一個三等分點時,
的一個三等分點時, 平面
平面 .
.
20.解:(Ⅰ)設等差數列 的公差為
的公差為 ,
,
則 ,
,
(Ⅱ)由
得 ,故數列
,故數列 適合條件①
適合條件①
而 ,則當
,則當 或
或 時,
時, 有最大值20
有最大值20
即 ,故數列
,故數列 適合條件②.
適合條件②.
綜上,故數列 是“特界”數列。
是“特界”數列。
21. 證明:
證明: 消去
消去 得
得

設點 ,則
,則 ,
,
由 ,
, ,即
,即
化簡得 ,則
,則
即 ,故
,故
(Ⅱ)解:由
化簡得
由 得
得 ,即
,即
故橢圓的長軸長的取值范圍是 。
。
22.解:(Ⅰ) ,由
,由 在區間
在區間 上是增函數
上是增函數
則當 時,恒有
時,恒有 ,
,
即 在區間
在區間 上恒成立。
上恒成立。
由 且
且 ,解得
,解得 .
.
(Ⅱ)依題意得
則 ,解得
,解得
而
故 在區間
在區間 上的最大值是
上的最大值是 。
。
(Ⅲ)若函數 的圖象與函數
的圖象與函數 的圖象恰有3個不同的交點,
的圖象恰有3個不同的交點,
即方程 恰有3個不等的實數根。
恰有3個不等的實數根。
而 是方程
是方程 的一個實數根,則
的一個實數根,則
方程 有兩個非零實數根,
有兩個非零實數根,
則 即
即 且
且 .
.
故滿足條件的 存在,其取值范圍是
存在,其取值范圍是 .
.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com