
題目列表(包括答案和解析)
| 2 |

 (1)下列說法正確的是
(1)下列說法正確的是1.[物理——選修2-2] (1)常見的傳動方式有__________、__________、__________和齒輪傳動等。齒輪傳動的傳動比是主動輪與__________的轉速之比,傳動比等于__________與__________的齒數之比。
(2)液壓千斤頂是利用密閉容器內的液體能夠把液體所受到的壓強向各個方向傳遞的原理制成的。圖為一小型千斤頂的結構示意圖。大活塞A的直徑D1=20 cm,小活塞B的直徑D2=5 cm,手柄的長度OC=50 cm,小活塞與手柄的連接點到轉軸O的距離DO=10 cm。現用此千斤頂使質量m=4×103 kg的重物升高了h=10 cm。g取10 m/s2,求
(i)若此千斤頂的效率為80%,在這一過程中人做的功為多少?
(ii)若此千斤頂的效率為100%,當重物上升時,人對手柄的作用力F至少要多大?
2.[物理——選修3-3]
(1)帶有活塞的氣缸內封閉一定量的理想氣體。氣體開始處于狀態a,然后經過過程ab到達狀態b或經過過程ac到達狀態c,b、c狀態溫度相同,如V-T圖所示。設氣體在狀態b和狀態c的壓強分別為pb和pc,在過程ab和ac中吸收的熱量分別為Qab和Qac,則___________(填入選項前的字母,有填錯的不得分)
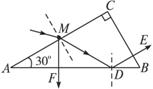
A.pb>pc,Qab>Qac B.pb>pc,Qab<Qac
C.pb<pc,Qab>Qac D.pb<pc,Qab<Qac
(2)圖中系統由左右兩個側壁絕熱、底部導熱、截面均為S的容器組成。左容器足夠高,上端敞開,右容器上端由導熱材料封閉。兩容器的下端由可忽略容積的細管連通。
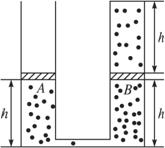
容器內兩個絕熱的活塞A、B下方封有氮氣,B上方封有氫氣。大氣的壓強為p0,溫度為T0=273 K,兩活塞因自身重量對下方氣體產生的附加壓強均為0.1p0。系統平衡時,各氣柱的高度如圖所示。現將系統底部浸入恒溫熱水槽中,再次平衡時A上升了一定高度。用外力將A緩慢推回第一次平衡時的位置并固定,第三次達到平衡后,氫氣柱高度為0.8h。氮氣和氫氣均可視為理想氣體。求
(i)第二次平衡時氮氣的體積;
(ii)水的溫度。
3.[物理——選修3-4]
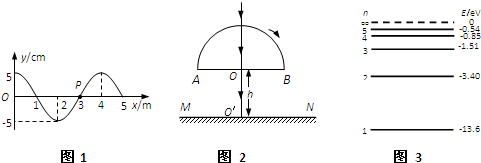
(1)某振動系統的固有頻率為f0,在周期性驅動力的作用下做受迫振動,驅動力的頻率為f。若驅動力的振幅保持不變,下列說法正確的是______(填入選項前的字母,有填錯的不得分)
A.當f<f0時,該振動系統的振幅隨f增大而減小
B.當f>f0時,該振動系統的振幅隨f減小而增大
C.該振動系統的振動穩定后,振動的頻率等于f0
D.該振動系統的振動穩定后,振動的頻率等于f
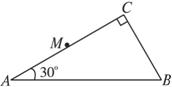
(2)一棱鏡的截面為直角三角形ABC,∠A=30°,斜邊AB=a。棱鏡材料的折射率為![]() 。在此截面所在的平面內,一條光線以45°的入射角從AC邊的中點M射入棱鏡。畫出光路圖,并求光線從棱鏡射出的點的位置(不考慮光線沿原路返回的情況)。
。在此截面所在的平面內,一條光線以45°的入射角從AC邊的中點M射入棱鏡。畫出光路圖,并求光線從棱鏡射出的點的位置(不考慮光線沿原路返回的情況)。
4.[物理——選修3-5]
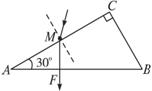
(1)關于光電效應,下列說法正確的是________(填入選項前的字母,有填錯的不得分)
A.極限頻率越大的金屬材料逸出功越大
B.只要光照射的時間足夠長,任何金屬都能產生光電效應
C.從金屬表面出來的光電子的最大初動能越大,這種金屬的逸出功越小
D.入射光的光強一定時,頻率越高,單位時間內逸出的光電子數就越多
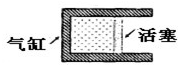
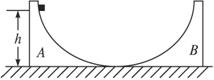
(2)兩個質量分別為M1和M2的劈A和B,高度相同,放在光滑水平面上。A和B的傾斜面都是光滑曲面,曲面下端與水平面相切,如圖所示。一質量為m的物塊位于劈A的傾斜面上,距水平面的高度為h。物塊從靜止開始滑下,然后又滑上劈B。求物塊在B上能夠達到的最大高度。
第七部分 熱學
熱學知識在奧賽中的要求不以深度見長,但知識點卻非常地多(考綱中羅列的知識點幾乎和整個力學——前五部分——的知識點數目相等)。而且,由于高考要求對熱學的要求逐年降低(本屆尤其低得“離譜”,連理想氣體狀態方程都沒有了),這就客觀上給奧賽培訓增加了負擔。因此,本部分只能采新授課的培訓模式,將知識點和例題講解及時地結合,爭取讓學員學一點,就領會一點、鞏固一點,然后再層疊式地往前推進。
一、分子動理論
1、物質是由大量分子組成的(注意分子體積和分子所占據空間的區別)
對于分子(單原子分子)間距的計算,氣體和液體可直接用![]() ,對固體,則與分子的空間排列(晶體的點陣)有關。
,對固體,則與分子的空間排列(晶體的點陣)有關。

【例題1】如圖6-1所示,食鹽(NaCl)的晶體是由鈉離子(圖中的白色圓點表示)和氯離子(圖中的黑色圓點表示)組成的,離子鍵兩兩垂直且鍵長相等。已知食鹽的摩爾質量為58.5×10-3kg/mol,密度為2.2×103kg/m3,阿伏加德羅常數為6.0×1023mol-1,求食鹽晶體中兩個距離最近的鈉離子中心之間的距離。
【解說】題意所求即圖中任意一個小立方塊的變長(設為a)的![]() 倍,所以求a成為本題的焦點。
倍,所以求a成為本題的焦點。
由于一摩爾的氯化鈉含有NA個氯化鈉分子,事實上也含有2NA個鈉離子(或氯離子),所以每個鈉離子占據空間為 v = ![]()
而由圖不難看出,一個離子占據的空間就是小立方體的體積a3 ,
即 a3 = ![]() =
= ![]() ,最后,鄰近鈉離子之間的距離l =
,最后,鄰近鈉離子之間的距離l = ![]() a
a
【答案】3.97×10-10m 。
〖思考〗本題還有沒有其它思路?
〖答案〗每個離子都被八個小立方體均分,故一個小立方體含有![]() ×8個離子 =
×8個離子 = ![]() 分子,所以…(此法普遍適用于空間點陣比較復雜的晶體結構。)
分子,所以…(此法普遍適用于空間點陣比較復雜的晶體結構。)
2、物質內的分子永不停息地作無規則運動
固體分子在平衡位置附近做微小振動(振幅數量級為0.1![]() ),少數可以脫離平衡位置運動。液體分子的運動則可以用“長時間的定居(振動)和短時間的遷移”來概括,這是由于液體分子間距較固體大的結果。氣體分子基本“居無定所”,不停地遷移(常溫下,速率數量級為102m/s)。
),少數可以脫離平衡位置運動。液體分子的運動則可以用“長時間的定居(振動)和短時間的遷移”來概括,這是由于液體分子間距較固體大的結果。氣體分子基本“居無定所”,不停地遷移(常溫下,速率數量級為102m/s)。
無論是振動還是遷移,都具備兩個特點:a、偶然無序(雜亂無章)和統計有序(分子數比率和速率對應一定的規律——如麥克斯韋速率分布函數,如圖6-2所示);b、劇烈程度和溫度相關。

氣體分子的三種速率。最可幾速率vP :f(v) = ![]() (其中ΔN表示v到v +Δv內分子數,N表示分子總數)極大時的速率,vP =
(其中ΔN表示v到v +Δv內分子數,N表示分子總數)極大時的速率,vP =![]() =
=![]() ;平均速率
;平均速率![]() :所有分子速率的算術平均值,
:所有分子速率的算術平均值,![]() =
=![]() =
=![]() ;方均根速率
;方均根速率![]() :與分子平均動能密切相關的一個速率,
:與分子平均動能密切相關的一個速率,![]() =
=![]() =
=![]() 〔其中R為普適氣體恒量,R = 8.31J/(mol.K)。k為玻耳茲曼常量,k =
〔其中R為普適氣體恒量,R = 8.31J/(mol.K)。k為玻耳茲曼常量,k = ![]() = 1.38×10-23J/K 〕
= 1.38×10-23J/K 〕
【例題2】證明理想氣體的壓強P = ![]() n
n![]() ,其中n為分子數密度,
,其中n為分子數密度,![]() 為氣體分子平均動能。
為氣體分子平均動能。

【證明】氣體的壓強即單位面積容器壁所承受的分子的撞擊力,這里可以設理想氣體被封閉在一個邊長為a的立方體容器中,如圖6-3所示。
考查yoz平面的一個容器壁,P = ![]() ①
①
設想在Δt時間內,有Nx個分子(設質量為m)沿x方向以恒定的速率vx碰撞該容器壁,且碰后原速率彈回,則根據動量定理,容器壁承受的壓力
F =![]() =
=![]() ②
②
在氣體的實際狀況中,如何尋求Nx和vx呢?
考查某一個分子的運動,設它的速度為v ,它沿x、y、z三個方向分解后,滿足
v2 = ![]() +
+ ![]() +
+ ![]()
分子運動雖然是雜亂無章的,但仍具有“偶然無序和統計有序”的規律,即
![]() =
= ![]() +
+ ![]() +
+ ![]() = 3
= 3![]() ③
③
這就解決了vx的問題。另外,從速度的分解不難理解,每一個分子都有機會均等的碰撞3個容器壁的可能。設Δt = ![]() ,則
,則
Nx = ![]() ·3N總 =
·3N總 = ![]() na3 ④
na3 ④
注意,這里的![]() 是指有6個容器壁需要碰撞,而它們被碰的幾率是均等的。
是指有6個容器壁需要碰撞,而它們被碰的幾率是均等的。

結合①②③④式不難證明題設結論。
〖思考〗此題有沒有更簡便的處理方法?
〖答案〗有。“命令”所有分子以相同的速率v沿+x、?x、+y、?y、+z、?z這6個方向運動(這樣造成的宏觀效果和“雜亂無章”地運動時是一樣的),則 Nx =![]() N總 =
N總 = ![]() na3 ;而且vx = v
na3 ;而且vx = v
所以,P = ![]() =
= ![]() =
= =
=![]() nm
nm![]() =
= ![]() n
n![]()
3、分子間存在相互作用力(注意分子斥力和氣體分子碰撞作用力的區別),而且引力和斥力同時存在,宏觀上感受到的是其合效果。
分子力是保守力,分子間距改變時,分子力做的功可以用分子勢能的變化表示,分子勢能EP隨分子間距的變化關系如圖6-4所示。
分子勢能和動能的總和稱為物體的內能。
二、熱現象和基本熱力學定律
1、平衡態、狀態參量
a、凡是與溫度有關的現象均稱為熱現象,熱學是研究熱現象的科學。熱學研究的對象都是有大量分子組成的宏觀物體,通稱為熱力學系統(簡稱系統)。當系統的宏觀性質不再隨時間變化時,這樣的狀態稱為平衡態。
b、系統處于平衡態時,所有宏觀量都具有確定的值,這些確定的值稱為狀態參量(描述氣體的狀態參量就是P、V和T)。
c、熱力學第零定律(溫度存在定律):若兩個熱力學系統中的任何一個系統都和第三個熱力學系統處于熱平衡狀態,那么,這兩個熱力學系統也必定處于熱平衡。這個定律反映出:處在同一熱平衡狀態的所有的熱力學系統都具有一個共同的宏觀特征,這一特征是由這些互為熱平衡系統的狀態所決定的一個數值相等的狀態函數,這個狀態函數被定義為溫度。
2、溫度
a、溫度即物體的冷熱程度,溫度的數值表示法稱為溫標。典型的溫標有攝氏溫標t、華氏溫標F(F = ![]() t + 32)和熱力學溫標T(T = t + 273.15)。
t + 32)和熱力學溫標T(T = t + 273.15)。
b、(理想)氣體溫度的微觀解釋:![]() =
= ![]() kT (i為分子的自由度 = 平動自由度t + 轉動自由度r + 振動自由度s 。對單原子分子i = 3 ,“剛性”〈忽略振動,s = 0,但r = 2〉雙原子分子i = 5 。對于三個或三個以上的多原子分子,i = 6 。能量按自由度是均分的),所以說溫度是物質分子平均動能的標志。
kT (i為分子的自由度 = 平動自由度t + 轉動自由度r + 振動自由度s 。對單原子分子i = 3 ,“剛性”〈忽略振動,s = 0,但r = 2〉雙原子分子i = 5 。對于三個或三個以上的多原子分子,i = 6 。能量按自由度是均分的),所以說溫度是物質分子平均動能的標志。
c、熱力學第三定律:熱力學零度不可能達到。(結合分子動理論的觀點2和溫度的微觀解釋很好理解。)
3、熱力學過程
a、熱傳遞。熱傳遞有三種方式:傳導(對長L、橫截面積S的柱體,Q = K![]() SΔ
SΔ
1.D 2.AD 3.BD 4.D 5. C 6.AD 7.B 8.AD 9.AD 10.B
11. 100J 75J 12. 15N
13. 解:設卡車運動的速度為v0,剎車后至停止運動,由動能定理:-μmgs=0-動能定理與能量守恒.files/image345.gif) 。得v=
。得v=動能定理與能量守恒.files/image347.gif) =
=
14. 解:當人向右勻速前進的過程中,繩子與豎直
方向的夾角由0°逐漸增大,人的拉力就發生了變化,
故無法用W=Fscosθ計算拉力所做的功,而在這個過
動能定理與能量守恒.files/image348.gif) 程中,人的拉力對物體做的功使物體的動能發生了變
程中,人的拉力對物體做的功使物體的動能發生了變
化,故可以用動能定理來計算拉力做的功。
當人在滑輪的正下方時,物體的初速度為零,
當人水平向右勻速前進s 時物體的速度為v1 ,由圖
1可知: v1= v0sina
⑴根據動能定理,人的拉力對物體所做的功
W=m v12/2-0
⑵由⑴、⑵兩式得W=ms2 v12/2(s2+h2)
15. 解:(1)對AB段應用動能定理:mgR+Wf=動能定理與能量守恒.files/image350.gif)
所以:Wf=動能定理與能量守恒.files/image350.gif) -mgR=
-mgR=動能定理與能量守恒.files/image353.gif) -20×10-3×10×1=-0.11J
-20×10-3×10×1=-0.11J
(2)對BC段應用動能定理:Wf=0-動能定理與能量守恒.files/image350.gif) =-
=-動能定理與能量守恒.files/image353.gif) =-0.09J。又因Wf=μmgBCcos1800=-0.09,得:μ=0.153。
=-0.09J。又因Wf=μmgBCcos1800=-0.09,得:μ=0.153。
16. 解:在此過程中,B的重力勢能的增量為動能定理與能量守恒.files/image355.gif) ,A、B動能增量為
,A、B動能增量為動能定理與能量守恒.files/image357.gif) ,恒力F所做的功為
,恒力F所做的功為動能定理與能量守恒.files/image359.gif) ,用
,用動能定理與能量守恒.files/image361.gif) 表示A克服摩擦力所做的功,根據功能關系有:
表示A克服摩擦力所做的功,根據功能關系有:
動能定理與能量守恒.files/image363.gif)
解得:動能定理與能量守恒.files/image365.gif)
17. 解:(1)兒童從A點滑到E點的過程中,重力做功W=mgh
兒童由靜止開始滑下最后停在E點,在整個過程中克服摩擦力做功W1,由動能定理得,
動能定理與能量守恒.files/image367.gif) =0,則克服摩擦力做功為W1=mgh
=0,則克服摩擦力做功為W1=mgh
(2)設斜槽AB與水平面的夾角為動能定理與能量守恒.files/image369.gif) ,兒童在斜槽上受重力mg、支持力N1和滑動摩擦
,兒童在斜槽上受重力mg、支持力N1和滑動摩擦
力f1,動能定理與能量守恒.files/image371.gif) ,兒童在水平槽上受重力mg、支持力N2和滑動摩擦力f2,
,兒童在水平槽上受重力mg、支持力N2和滑動摩擦力f2,
動能定理與能量守恒.files/image373.gif) ,兒童從A點由靜止滑下,最后停在E點.
,兒童從A點由靜止滑下,最后停在E點.
由動能定理得,動能定理與能量守恒.files/image375.gif)
解得動能定理與能量守恒.files/image377.gif) ,它與角
,它與角動能定理與能量守恒.files/image379.gif) 無關.
無關.
(3)兒童沿滑梯滑下的過程中,通過B點的速度最大,顯然,傾角動能定理與能量守恒.files/image381.gif) 越大,通過B點的速度越大,設傾角為
越大,通過B點的速度越大,設傾角為動能定理與能量守恒.files/image383.gif) 時有最大速度v,由動能定理得,
時有最大速度v,由動能定理得,
動能定理與能量守恒.files/image385.gif)
解得最大傾角動能定理與能量守恒.files/image387.gif)
18.
解:(1)根據牛頓第二定律有:動能定理與能量守恒.files/image389.gif)
設勻加速的末速度為動能定理與能量守恒.files/image063.gif) ,則有:
,則有:動能定理與能量守恒.files/image392.gif) 、
、動能定理與能量守恒.files/image394.gif)
代入數值,聯立解得:勻加速的時間為:動能定理與能量守恒.files/image396.gif)
(2)當達到最大速度動能定理與能量守恒.files/image087.gif) 時,有:
時,有:動能定理與能量守恒.files/image399.gif)
解得:汽車的最大速度為:動能定理與能量守恒.files/image401.gif)
(3)汽車勻加速運動的位移為:動能定理與能量守恒.files/image403.gif)
在后一階段牽引力對汽車做正功,重力和阻力做負功,根據動能定理有:
動能定理與能量守恒.files/image405.gif)
又有動能定理與能量守恒.files/image407.gif)
代入數值,聯立求解得:動能定理與能量守恒.files/image409.gif)
所以汽車總的運動時間為:動能定理與能量守恒.files/image411.gif)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com