
題目列表(包括答案和解析)
C
[解析] 依題意得![]() +
+![]() =(
=(![]() +
+![]() )[x+(1-x)]=13+
)[x+(1-x)]=13+![]() +
+![]() ≥13+2
≥13+2![]() =25,當且僅當
=25,當且僅當![]() =
=![]() ,即x=
,即x=![]() 時取等號,選C.
時取等號,選C.
在 中,已知
中,已知
 ,面積
,面積 ,
,
(1)求 的三邊的長;
的三邊的長;
(2)設 是
是 (含邊界)內的一點,
(含邊界)內的一點, 到三邊
到三邊 的距離分別是
的距離分別是
①寫出 所滿足的等量關系;
所滿足的等量關系;
②利用線性規劃相關知識求出 的取值范圍.
的取值范圍.
【解析】第一問中利用設 中角
中角 所對邊分別為
所對邊分別為
由 得
得
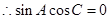

又由 得
得 即
即

又由 得
得 即
即

又
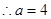 又
又 得
得
即 的三邊長
的三邊長

第二問中,① 得
得

故
②
令 依題意有
依題意有
作圖,然后結合區域得到最值。

已知數列 是公差不為零的等差數列,
是公差不為零的等差數列,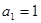 ,且
,且 、
、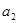 、
、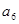 成等比數列。
成等比數列。
⑴求數列 的通項公式;
的通項公式;
⑵設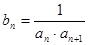 ,求數列
,求數列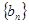 的前
的前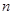 項和
項和 。
。
【解析】第一問中利用等差數列 的首項為
的首項為 ,公差為d,則依題意有:
,公差為d,則依題意有:
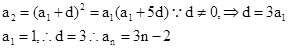
第二問中,利用第一問的結論得到數列的通項公式,
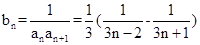 ,利用裂項求和的思想解決即可。
,利用裂項求和的思想解決即可。
在 中,
中, 是三角形的三內角,
是三角形的三內角, 是三內角對應的三邊,已知
是三內角對應的三邊,已知 成等差數列,
成等差數列, 成等比數列
成等比數列
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
【解析】第一問中利用依題意 且
且 ,故
,故
第二問中,由題意 又由余弦定理知
又由余弦定理知

,得到 ,所以
,所以 ,從而得到結論。
,從而得到結論。
(1)依題意 且
且 ,故
,故 ……………………6分
……………………6分
(2)由題意 又由余弦定理知
又由余弦定理知
 …………………………9分
…………………………9分
即 故
故

 代入
代入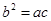 得
得

如圖, ,
,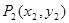 ,…,
,…, ,…是曲線
,…是曲線 上的點,
上的點, ,
, ,…,
,…, ,…是
,…是 軸正半軸上的點,且
軸正半軸上的點,且 ,
, ,…,
,…, ,…
均為斜邊在
,…
均為斜邊在 軸上的等腰直角三角形(
軸上的等腰直角三角形( 為坐標原點).
為坐標原點).
(1)寫出 、
、 和
和 之間的等量關系,以及
之間的等量關系,以及 、
、 和
和 之間的等量關系;
之間的等量關系;
(2)求證: (
( );
);
(3)設 ,對所有
,對所有 ,
, 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.

【解析】第一問利用有 ,
, 得到
得到
第二問證明:①當 時,可求得
時,可求得 ,命題成立;②假設當
,命題成立;②假設當 時,命題成立,即有
時,命題成立,即有 則當
則當 時,由歸納假設及
時,由歸納假設及 ,
,
得
第三問

 .………………………2分
.………………………2分
因為函數 在區間
在區間 上單調遞增,所以當
上單調遞增,所以當 時,
時, 最大為
最大為 ,即
,即

解:(1)依題意,有 ,
, ,………………4分
,………………4分
(2)證明:①當 時,可求得
時,可求得 ,命題成立;
……………2分
,命題成立;
……………2分
②假設當 時,命題成立,即有
時,命題成立,即有 ,……………………1分
,……………………1分
則當 時,由歸納假設及
時,由歸納假設及 ,
,
得 .
.
即
解得 (
( 不合題意,舍去)
不合題意,舍去)
即當 時,命題成立. …………………………………………4分
時,命題成立. …………………………………………4分
綜上所述,對所有 ,
, . ……………………………1分
. ……………………………1分
(3)

 .………………………2分
.………………………2分
因為函數 在區間
在區間 上單調遞增,所以當
上單調遞增,所以當 時,
時, 最大為
最大為 ,即
,即
 .……………2分
.……………2分
由題意,有
 .
所以,
.
所以,
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com