
題目列表(包括答案和解析)
| OC |
| OM |
| ON |
| OA |
| OB |
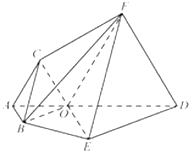 平面四邊形ABED中,O在線段AD上,且OA=1,OD=2,△OAB,△ODE都是正三角形.將四邊形ABED沿AD翻折后,使點B落在點C位置,點E落在點F位置,且F點在平面ABED上的射影恰為線段OD的中點(即垂線段的垂足點),所得多面體ABEDFC,如圖所示
平面四邊形ABED中,O在線段AD上,且OA=1,OD=2,△OAB,△ODE都是正三角形.將四邊形ABED沿AD翻折后,使點B落在點C位置,點E落在點F位置,且F點在平面ABED上的射影恰為線段OD的中點(即垂線段的垂足點),所得多面體ABEDFC,如圖所示 平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四邊形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=
平面ABDE⊥平面ABC,△ABC是等腰直角三角形,AC=BC=4,四邊形ABDE是直角梯形,BD∥AE,BD⊥BA,BD=| 1 | 2 |
()(本小題滿分12分)
如圖,四棱錐S-ABCD 的底面是正方形,每條側(cè)棱的長都是地面邊長的![]() 倍,P為側(cè)棱SD上的點。
倍,P為側(cè)棱SD上的點。 
(Ⅰ)求證:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的條件下,側(cè)棱SC上是否存在一點E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,試說明理由。
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com