
題目列表(包括答案和解析)
設![]() 的最大值為M。
的最大值為M。
(1)當![]() 時,求M的值。
時,求M的值。
(2)當![]() 取遍所有實數時,求M的最小值
取遍所有實數時,求M的最小值![]() ;
;
(以下結論可供參考:對于![]() ,當
,當![]() 同號時取等號)
同號時取等號)
(3)對于第(2)小題中的![]() ,設數列
,設數列![]() 滿足
滿足![]() ,求證:
,求證:![]() 。
。
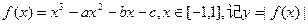 的最大值為M。
的最大值為M。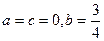 時,求M的值。
時,求M的值。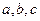 取遍所有實數時,求M的最小值
取遍所有實數時,求M的最小值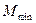 ;
;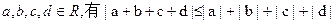 ,當
,當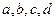 同號時取等號)
同號時取等號) ,設數列
,設數列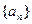 滿足
滿足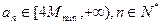 ,求證:
,求證: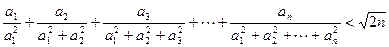 。
。已知函數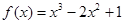 .
.
(1)求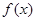 在區間
在區間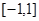 上的最大值;
上的最大值;
(2)若函數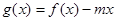 在區間
在區間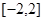 上存在遞減區間,求實數m的取值范圍.
上存在遞減區間,求實數m的取值范圍.
【解析】本試題主要考查了導數在研究函數中的運用,求解函數的最值。第一問中,利用導數求解函數的最值,首先求解導數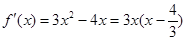 ,然后利用極值和端點值比較大小,得到結論。第二問中,我們利用函數在
,然后利用極值和端點值比較大小,得到結論。第二問中,我們利用函數在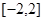 上存在遞減區間,即
上存在遞減區間,即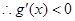 在
在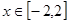 上有解,即
上有解,即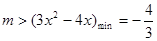 ,即可,可得到。
,即可,可得到。
解:(1)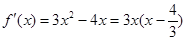 ,
,
令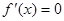 ,解得
,解得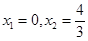 ……………3分
……………3分
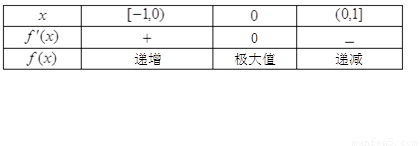
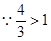 ,
,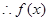 在
在 上為增函數,在
上為增函數,在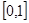 上為減函數,
上為減函數,
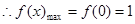 .
…………6分
.
…………6分
(2)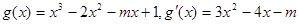
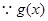 在
在 上存在遞減區間,
上存在遞減區間,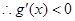 在
在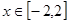 上有解,……9分
上有解,……9分
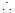
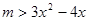 在
在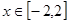 上有解,
上有解,
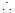
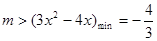 ,
,
所以,實數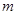 的取值范圍為
的取值范圍為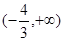
已知△ABC的三個內角A、B、C所對的邊分別為a、b、c,向量

(Ⅰ)求角A的大小;
(Ⅱ)若 ,試判斷b·c取得最大值時△ABC形狀.
,試判斷b·c取得最大值時△ABC形狀.
【解析】本試題主要考查了解三角形的運用。第一問中利用向量的數量積公式 ,且由
,且由
(2)問中利用余弦定理 ,以及
,以及 ,可知
,可知 ,并為等邊三角形。
,并為等邊三角形。
解:(Ⅰ)


 ………………………………6分
………………………………6分
(Ⅱ)
 ………………………………8分
………………………………8分

 ……………10分
……………10分

心理學研究表明,學生在課堂上各時段的接受能力不同。上課開始時,學生的興趣高昂,接受能力漸強,隨后有一段不太長的時間,學生的接受能力保持較理想的狀態;漸漸地學生的注意力開始分散,接受能力漸弱并趨于穩定.設上課開始![]() 分鐘時,學生的接受能力為
分鐘時,學生的接受能力為![]() (
(![]() 值越大,表示接受能力越強),
值越大,表示接受能力越強),![]() 與
與![]() 的函數關系為:
的函數關系為:
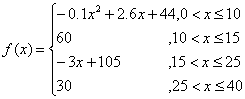
(1)開講后多少分鐘,學生的接受能力最強?能維持多少時間?
(2)試比較開講后5分鐘、20分鐘、35分鐘,學生的接受能力的大小;
(3)若一個數學難題,需要56的接受能力(即![]() )以及12分鐘時間,老師能否及時在學生一直達到所需接受能力的狀態下講述完這個難題?
)以及12分鐘時間,老師能否及時在學生一直達到所需接受能力的狀態下講述完這個難題?
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com