題目列表(包括答案和解析)
C．選修4-4：坐標系與參數方程
在極坐標系下，已知圓O：
和直線
，
（1）求圓O和直線
的直角坐標方程；（2）當
時，求直線與圓O公共點的一個極坐標.
D．選修4-5：不等式證明選講
對于任意實數
和
，不等式
恒成立，試求實數
的取值范圍．
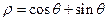和直線
，
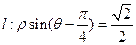的直角坐標方程；（2）當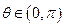
時，求直線與圓O公共點的一個極坐標.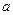
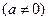和
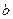，不等式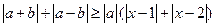
恒成立，試求實數
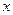的取值范圍．C
[解析] 由基本不等式，得ab≤
＝
＝
－ab，所以ab≤
，故B錯；
＋
＝
＝
≥4，故A錯；由基本不等式得
≤
＝
，即
＋
≤
，故C正確；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×＝，故D錯．故選C.
．定義域為R的函數
滿足
，且當
時，
，則當
時，
的最小值為（ ）
（A）
（B）
（C）
（D）
．過點
作圓
的弦，其中弦長為整數的共有 （ ）
A.16條 B. 17條 C. 32條 D. 34條
一、
二、
9．16 10．2009 11．
12．
13．
14．3 
15．②③
三、
16．解：（1）由余弦定理得： 
是以角C為直角的直角三角形.……………………6分
（2）
中
………………①
………………②
②÷①得
，
則
……………………12分
17．解：（1）因為
……………………………………（2分）
……………………………………………………（4分）
所以線路信息通暢的概率為
。………………………（6分）
（2）
的所有可能取值為4，5，6，7，8。
……………………………………………………………（9分）
∴
的分布列為
4
5
6
7
8
P
…………………………………………………………………………………………（10分）
∴E=4×+5×+6×+7×+8×=6。……………………（12分）
18．解：解法一：（1）證明：連結OC，
∵
ABD為等邊三角形，O為BD的中點，∴AO
垂直BD。………………………………………………………………（1分）
∴ AO=CO=
。………………………………………………………………………（2分）
在
AOC中，AC=
，∴AO2+CO2=AC2，
∴∠AOC=900，即AO⊥OC。
∴BD
OC=O，∴AO⊥平面BCD。…………………………………………………（3分）
（2）過O作OE垂直BC于E，連結AE，
∵AO⊥平面BCD，∴AE在平面BCD上的射影為OE。
∴AE⊥BC。
∠AEO為二面角A―BC―D的平面角。………………………………………（7分）
在Rt
AEO中，AO=，OE=
，
∠
，
∴∠AEO=arctan2。
二面角A―BC―D的大小為arctan2。
（3）設點O到面ACD的距離為
∵VO-ACD=VA-OCD，
∴
。
在ACD中，AD=CD=2，AC=，
。
|
。
。…………………（12分）
=(0,0,
)。…………………………………………（5分）
，
。設
與
，
。
。…………………………………………（8分）
又
。………………………………（11分）
與
夾角為
，則
,
.
…共線，該直線過點P1（a,a），
……………………3分
時，An是一個三角形與一個梯形面積之和（如上圖所示），梯形面積是
…………………………7分
，……………………10分
，
……………………13分
，
為正三角形，
……………………2分
），N（
），
得，
……………………4分
………………6分
且滿足上述方程，
………………7分
…………………………9分
……………………10分
面積的最大值為
…………………………13分
……………………3分
＞
＞
＞0,
≥
≥
≥
…（5分）
……………………7分
，
；………………9分
再三式作和即得
……………………13分