
題目列表(包括答案和解析)
如圖,在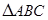 中,
中,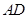 為
為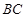 邊上的中線,
邊上的中線,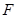 為
為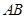 上任意一點,
上任意一點,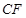 交
交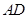 于點
于點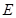 .求證:
.求證: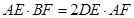 .
.
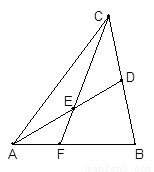
【解析】本試題主要是考查了平面幾何中相似三角形性質的運用。根據已知條件,首先做輔助線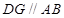 ,然后利用平行性得到相似比,
,然后利用平行性得到相似比,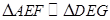 ,
,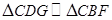 ,然后得到比例相等。充分利用比值問題轉化得到結論。
,然后得到比例相等。充分利用比值問題轉化得到結論。
證明:過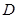 作
作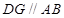 ,交
,交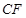 于
于 ,∴
,∴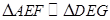 ,
,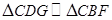 ,
,
∴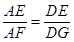 ,
,  , ∵
, ∵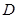 為
為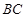 的中點,
的中點,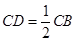 ,
,
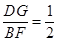 ,
,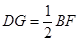 ,
,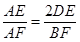 ,即
,即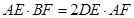 .
.
在 中,
中, 是三角形的三內角,
是三角形的三內角, 是三內角對應的三邊,已知
是三內角對應的三邊,已知 成等差數列,
成等差數列, 成等比數列
成等比數列
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求 的值.
的值.
【解析】第一問中利用依題意 且
且 ,故
,故
第二問中,由題意 又由余弦定理知
又由余弦定理知

,得到 ,所以
,所以 ,從而得到結論。
,從而得到結論。
(1)依題意 且
且 ,故
,故 ……………………6分
……………………6分
(2)由題意 又由余弦定理知
又由余弦定理知
 …………………………9分
…………………………9分
即 故
故

 代入
代入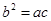 得
得

如圖,三棱柱 中,側棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中點。
中,側棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中點。

(I) 證明:平面 ⊥平面
⊥平面
(Ⅱ)平面 分此棱柱為兩部分,求這兩部分體積的比.
分此棱柱為兩部分,求這兩部分體積的比.
【命題意圖】本題主要考查空間線線、線面、面面垂直的判定與性質及幾何體的體積計算,考查空間想象能力、邏輯推理能力,是簡單題.
【解析】(Ⅰ)由題設知BC⊥ ,BC⊥AC,
,BC⊥AC, ,∴
,∴ 面
面 , 又∵
, 又∵
 面
面 ,∴
,∴ ,
,
由題設知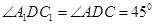 ,∴
,∴ =
= ,即
,即 ,
,
又∵ , ∴
, ∴ ⊥面
⊥面 , ∵
, ∵
 面
面 ,
,
∴面 ⊥面
⊥面 ;
;
(Ⅱ)設棱錐 的體積為
的體積為 ,
, =1,由題意得,
=1,由題意得, =
= =
= ,
,
由三棱柱 的體積
的體積 =1,
=1,
∴ =1:1, ∴平面
=1:1, ∴平面 分此棱柱為兩部分體積之比為1:1
分此棱柱為兩部分體積之比為1:1
近年來,某市為了促進生活垃圾的分類處理,將生活垃圾分為廚余垃圾、可回收物和其他垃圾三類,并分別設置了相應的垃圾箱。為調查居民生活垃圾分類投放情況,現隨機抽取了該市三類垃圾箱中總計1000噸生活垃圾,數據統計如下(單位:噸):
|
|
“廚余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
廚余垃圾 |
400 |
100 |
100 |
|
可回收物 |
30 |
240 |
30 |
|
其他垃圾 |
20 |
20 |
60 |
(Ⅰ)試估計廚余垃圾投放正確的概率
(Ⅱ)試估計生活垃圾投放錯誤的概率
(Ⅲ)假設廚余垃圾在“廚余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分別為a,b,c,其中a>0,a+b+c=600.當數據a,b,c,的方差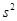 最大時,寫出a,b,c的值(結論不要求證明),并求此時
最大時,寫出a,b,c的值(結論不要求證明),并求此時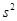 的值。
的值。
(注: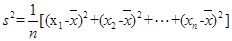 ,其中
,其中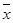 為數據
為數據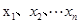 的平均數)
的平均數)
【解析】(1)廚余垃圾投放正確的概率約為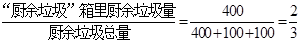
(2)設生活垃圾投放錯誤為事件A,則事件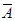 表示生活垃圾投放正確。事件
表示生活垃圾投放正確。事件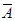 的概率約為“廚余垃圾”箱里廚余垃圾量、“可回收物”箱里可回收物量與“其他垃圾”箱里其他垃圾量的總和除以生活垃圾總量,即
的概率約為“廚余垃圾”箱里廚余垃圾量、“可回收物”箱里可回收物量與“其他垃圾”箱里其他垃圾量的總和除以生活垃圾總量,即 約為
約為 ,所以
,所以 約為
約為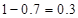
(3)當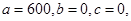 時,方差取得最大值,因為
時,方差取得最大值,因為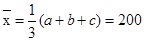 ,
,
所以
近年來,某市為了促進生活垃圾的分類處理,將生活垃圾分為廚余垃圾、可回收物和其他垃圾三類,并分別設置了相應的垃圾箱。為調查居民生活垃圾分類投放情況,現隨機抽取了該市三類垃圾箱中總計1000噸生活垃圾,數據統計如下(單位:噸):
|
|
“廚余垃圾”箱 |
“可回收物”箱 |
“其他垃圾”箱 |
|
廚余垃圾 |
400 |
100 |
100 |
|
可回收物 |
30 |
240 |
30 |
|
其他垃圾 |
20 |
20 |
60 |
(Ⅰ)試估計廚余垃圾投放正確的概率
(Ⅱ)試估計生活垃圾投放錯誤的概率
(Ⅲ)假設廚余垃圾在“廚余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分別為a,b,c,其中a>0,a+b+c=600.當數據a,b,c,的方差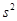 最大時,寫出a,b,c的值(結論不要求證明),并求此時
最大時,寫出a,b,c的值(結論不要求證明),并求此時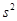 的值。
的值。
(注: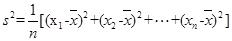 ,其中
,其中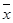 為數據
為數據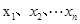 的平均數)
的平均數)
【解析】(1)廚余垃圾投放正確的概率約為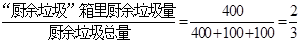
(2)設生活垃圾投放錯誤為事件A,則事件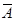 表示生活垃圾投放正確。事件
表示生活垃圾投放正確。事件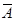 的概率約為“廚余垃圾”箱里廚余垃圾量、“可回收物”箱里可回收物量與“其他垃圾”箱里其他垃圾量的總和除以生活垃圾總量,即
的概率約為“廚余垃圾”箱里廚余垃圾量、“可回收物”箱里可回收物量與“其他垃圾”箱里其他垃圾量的總和除以生活垃圾總量,即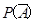 約為
約為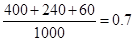 ,所以
,所以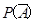 約為
約為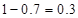
(3)當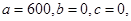 時,方差取得最大值,因為
時,方差取得最大值,因為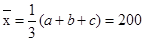 ,
,
所以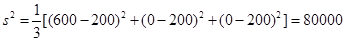
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com