
題目列表(包括答案和解析)
設(shè)函數(shù)f(x)的定義域為R,當(dāng)x<0時f(x)>1,且對任意的實數(shù)x,y∈R,有![]()
(Ⅰ)求f(0),判斷并證明函數(shù)f(x)的單調(diào)性;
(Ⅱ)數(shù)列![]() 滿足
滿足![]() ,且
,且![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
①求數(shù)列![]() 通項公式。
通項公式。
②求數(shù)列![]() 的前n項和Tn的最小值及相應(yīng)的n的值.
的前n項和Tn的最小值及相應(yīng)的n的值.
(本小題滿分12分)
定義在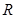 上的函數(shù)
上的函數(shù)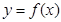 ,對于任意的實數(shù)
,對于任意的實數(shù)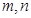 ,恒有
,恒有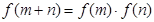 ,且當(dāng)
,且當(dāng)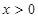 時,
時,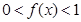 。
。
(1)求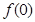 及
及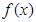 的值域。
的值域。
(2)判斷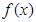 在
在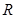 上的單調(diào)性,并證明。
上的單調(diào)性,并證明。
(3)設(shè)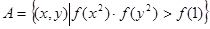 ,
,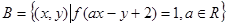 ,
,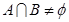 ,求
,求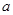 的范圍。
的范圍。
仔細(xì)閱讀下面問題的解法:
設(shè)A=[0, 1],若不等式21-x-a>0在A上有解,求實數(shù)a的取值范圍。
解:由已知可得 a < 21-x
令f(x)= 21-x ,∵不等式a <21-x在A上有解,
∴a <f(x)在A上的最大值.
又f(x)在[0,1]上單調(diào)遞減,f(x)max =f(0)=2. ∴實數(shù)a的取值范圍為a<2.
研究學(xué)習(xí)以上問題的解法,請解決下面的問題:
(1)已知函數(shù)f(x)=x2+2x+3(-2≤x≤-1),求f(x)的反函數(shù)及反函數(shù)的定義域A;
(2)對于(1)中的A,設(shè)g(x)=![]() ,x∈A,試判斷g(x)的單調(diào)性(寫明理由,不必證明);
,x∈A,試判斷g(x)的單調(diào)性(寫明理由,不必證明);
(3)若B ={x|![]() >2x+a–5},且對于(1)中的A,A∩B≠F,求實數(shù)a的取值范圍。
>2x+a–5},且對于(1)中的A,A∩B≠F,求實數(shù)a的取值范圍。
![]()
(北京市西城外語學(xué)校·2010屆高三測試)設(shè)函數(shù)f(x)的定義域為R,當(dāng)x<0時f(x)>1,且對任意的實數(shù)x,y∈R,有![]()
(Ⅰ)求f(0),判斷并證明函數(shù)f(x)的單調(diào)性;
(Ⅱ)數(shù)列![]() 滿足
滿足![]() ,且
,且![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]()
①求數(shù)列![]() 通項公式。
通項公式。
②求數(shù)列![]() 的前n項和Tn的最小值及相應(yīng)的n的值.
的前n項和Tn的最小值及相應(yīng)的n的值.
(本題16分)已知函數(shù) 在定義域
在定義域 上是奇函數(shù),(其中
上是奇函數(shù),(其中 且
且 ).
).
(1)求出 的值,并求出定義域
的值,并求出定義域 ;
;
(2)判斷 在
在 上的單調(diào)性,并用定義加以證明;
上的單調(diào)性,并用定義加以證明;
(3)當(dāng) 時,
時, 的值域范圍恰為
的值域范圍恰為 ,求
,求 及
及 的值.
的值.
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com