
題目列表(包括答案和解析)
解:(1)點C的坐標為![]() .
.
∵ 點A、B的坐標分別為![]() ,
,
∴ 可設過A、B、C三點的拋物線的解析式為![]() .
.
將![]() 代入拋物線的解析式,得
代入拋物線的解析式,得![]() .
.
∴ 過A、B、C三點的拋物線的解析式為![]() .
.
 (2)可得拋物線的對稱軸為
(2)可得拋物線的對稱軸為![]() ,頂點D的坐標為
,頂點D的坐標為
![]() ,設拋物線的對稱軸與x軸的交點為G.
,設拋物線的對稱軸與x軸的交點為G.
直線BC的解析式為![]() .
.
設點P的坐標為![]() .
.
解法一:如圖8,作OP∥AD交直線BC于點P,
連結AP,作PM⊥x軸于點M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ![]() ,即
,即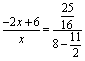 .
.
解得![]() . 經檢驗
. 經檢驗![]() 是原方程的解.
是原方程的解.
此時點P的坐標為![]() .
.
但此時![]() ,OM<GA.
,OM<GA.
∵ ![]()
∴ OP<AD,即四邊形的對邊OP與AD平行但不相等,
∴ 直線BC上不存在符合條件的點P. - - - - - - - - - - - - - - - - - - - - - 6分
解法二:如圖9,取OA的中點E,作點D關于點E的對稱點P,作PN⊥x軸于
點N. 則∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由![]() ,可得E點的坐標為
,可得E點的坐標為![]() .
.
NE=EG=![]() , ON=OE-NE=
, ON=OE-NE=![]() ,NP=DG=
,NP=DG=![]() .
.
∴ 點P的坐標為![]() .∵ x=
.∵ x=![]() 時,
時,![]() ,
,
∴ 點P不在直線BC上.
∴ 直線BC上不存在符合條件的點P .

(3)![]() 的取值范圍是
的取值范圍是![]() .
.
 (2012•柳州)如圖,在△ABC中,AB=2,AC=BC=
(2012•柳州)如圖,在△ABC中,AB=2,AC=BC=| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| x2-2 |
| x2-2 |
| x2-x1 |
| 2 |
| x1+x2 |
| 2 |
| y2-y1 |
| 2 |
| y1+y2 |
| 2 |
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

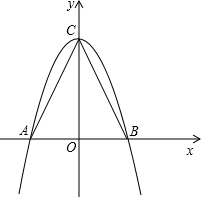
如圖,在△ABC中,AB=2,AC="BC=" 5 .
(1)以AB所在的直線為x軸,AB的垂直平分線為y軸,建立直角坐標系如圖,請你分別寫出A、B、C三點的坐標;
(2)求過A、B、C三點且以C為頂點的拋物線的解析式;
(3)若D為拋物線上的一動點,當D點坐標為何值時,S△ABD= S△ABC;
S△ABC;
(4)如果將(2)中的拋物線向右平移,且與x軸交于點A′B′,與y軸交于點C′,當平移多少個單位時,點C′同時在以A′B′為直徑的圓上(解答過程如果有需要時,請參看閱讀材料).
附:閱讀材料
一元二次方程常用的解法有配方法、公式法和因式分解法,對于一些特殊方程可以通過換元法轉化為一元二次方程求解.如解方程:y4-4y2+3=0.
解:令y2=x(x≥0),則原方程變為x2-4x+3=0,解得x1=1,x2=3.
當x1=1時,即y2=1,∴y1=1,y2=-1.
當x2=3,即y2=3,∴y3=" 3" ,y4="-" 3 .
所以,原方程的解是y1=1,y2=-1,y3=" 3" ,y4="-" 3 .
再如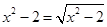 ,可設
,可設 ,用同樣的方法也可求解.
,用同樣的方法也可求解.
如圖,在直角坐標系中,![]() 是原點,
是原點,![]() 三點的坐標分別
三點的坐標分別![]() ,四邊形
,四邊形![]() 是梯形,點
是梯形,點![]() 同時從原點出發,分別作勻速運動,其中點
同時從原點出發,分別作勻速運動,其中點![]() 沿
沿![]() 向終點
向終點![]() 運動,速度為每秒
運動,速度為每秒![]() 個單位,點
個單位,點![]() 沿
沿![]() 向終點
向終點![]() 運動,當這兩點有一點到達自己的終點時,另一點也停止運動.
運動,當這兩點有一點到達自己的終點時,另一點也停止運動.
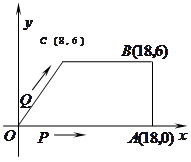
(1)求直線![]() 的解析式.
的解析式.
(2)設從出發起,運動了![]() 秒.如果點
秒.如果點![]() 的速度為每秒
的速度為每秒![]() 個單位,試寫出點
個單位,試寫出點![]() 的坐標,并寫出此時
的坐標,并寫出此時![]() 的取值范圍.
的取值范圍.
(3)設從出發起,運動了![]() 秒.當
秒.當![]() ,
,![]() 兩點運動的路程之和恰好等于梯形
兩點運動的路程之和恰好等于梯形![]() 的周長的一半,這時,直線
的周長的一半,這時,直線![]() 能否把梯形的面積也分成相等的兩部分,如有可能,請求出
能否把梯形的面積也分成相等的兩部分,如有可能,請求出![]() 的值;如不可能,請說明理由.
的值;如不可能,請說明理由.
【解析】(1)根據待定系數法就可以求出直線OC的解析式(2)本題應分Q在OC上,和在CB上兩種情況進行討論.即0≤t≤5和5<t≤10兩種情況(3)P、Q兩點運動的路程之和可以用t表示出來,梯形OABC的周長就可以求得.當P、Q兩點運動的路程之和恰好等于梯形OABC的周長的一半,就可以得到一個關于t的方程,可以解出t的值.梯形OABC的面積可以求出,梯形OCQP的面積可以用t表示出來.把t代入可以進行檢驗
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com