
題目列表(包括答案和解析)
如圖,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M為AA1的中點,P是BC上一點,且由P沿棱柱側面經過棱CC1到M點的最短路線長為![]() ,設這條最短路線與C1C的交點為N。求
,設這條最短路線與C1C的交點為N。求
1) 該三棱柱的側面展開圖的對角線長;
2) PC和NC的長;
3)  平面NMP和平面ABC所成二面角(銳角)的大小(用反三角函數表示)
平面NMP和平面ABC所成二面角(銳角)的大小(用反三角函數表示)

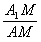 的值;
的值; 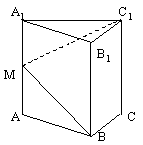

(本題滿分14分)
如圖所示,在正三棱柱ABC -A1B1C1中,底面邊長和側棱長都是2,D是側棱CC1上任意一點,E是A1B1的中點。
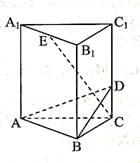
(I)求證:A1B1//平面ABD;
(II)求證:AB⊥CE;
(III)求三棱錐C-ABE的體積。
(本題滿分14分)
如圖所示,在正三棱柱ABC -A1B1C1中,底面邊長和側棱長都是2,D是側棱CC1上任意一點,E是A1B1的中點。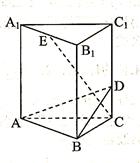
(I)求證:A1B1//平面ABD;
(II)求證:AB⊥CE;
(III)求三棱錐C-ABE的體積。
必修
一、填空題
1、8
2、二十世紀.files/image118.gif) 3、2|P|
4、
3、2|P|
4、二十世紀.files/image120.gif) 5、向左移
5、向左移二十世紀.files/image122.gif) ,在把各點的橫坐標伸長到原來的3倍
,在把各點的橫坐標伸長到原來的3倍
6、18
7、120度 8、二十世紀.files/image124.gif) 9、
9、二十世紀.files/image126.gif) 10、②④ 11、
10、②④ 11、二十世紀.files/image128.gif) 12、
12、二十世紀.files/image130.gif) 13、
13、二十世紀.files/image132.gif) 14、
14、二十世紀.files/image134.gif)
二、解答題
15.解:(Ⅰ)二十世紀.files/image136.gif) =
=二十世紀.files/image138.gif) .………… 4分
.………… 4分
由二十世紀.files/image140.gif) ,得
,得二十世紀.files/image142.gif) .
.
∴函數二十世紀.files/image144.gif) 的單調增區間為
的單調增區間為
二十世紀.files/image146.gif) .………… 7分
.………… 7分
(Ⅱ)由二十世紀.files/image148.gif) ,得
,得二十世紀.files/image150.gif) .
.
∴二十世紀.files/image152.gif) .
………………………………………… 10分
.
………………………………………… 10分
∴二十世紀.files/image154.gif) ,或
,或二十世紀.files/image156.gif)
二十世紀.files/image158.gif) ,
,
即二十世紀.files/image160.gif) 或
或二十世紀.files/image162.gif)
二十世紀.files/image158.gif) .
.
∵二十世紀.files/image164.gif) ,∴
,∴二十世紀.files/image166.gif) . …………………………………………… 14分
. …………………………………………… 14分
16.解:(Ⅰ)n≥2時,二十世紀.files/image168.gif) . ………………… 4分
. ………………… 4分
n=1時,二十世紀.files/image170.gif) ,適合上式,
,適合上式,
∴二十世紀.files/image168.gif)
二十世紀.files/image172.gif) .
………………… 5分
.
………………… 5分
(Ⅱ)二十世紀.files/image174.gif) ,
,二十世紀.files/image176.gif) .
………………… 8分
.
………………… 8分
即二十世紀.files/image178.gif) .
.
∴數列二十世紀.files/image180.gif) 是首項為4、公比為2的等比數列. ………………… 10分
是首項為4、公比為2的等比數列. ………………… 10分
二十世紀.files/image182.gif) ,∴
,∴二十世紀.files/image184.gif)
二十世紀.files/image186.gif) .……………… 12分
.……………… 12分
Tn=二十世紀.files/image188.gif) =
=二十世紀.files/image190.gif) . ………………… 14分
. ………………… 14分
17、⑴ ⑵ ⑶不能
18、⑴二十世紀.files/image192.gif)
⑵二十世紀.files/image194.gif) =1時,
=1時,二十世紀.files/image196.gif) 的最大值為20200,
的最大值為20200,二十世紀.files/image194.gif) =10時,
=10時,二十世紀.files/image196.gif) 的最小值為12100。
的最小值為12100。
19、⑴易知AB恒過橢圓的右焦點F(二十世紀.files/image110.gif) ,0) ⑵ S=
,0) ⑵ S= 二十世紀.files/image201.gif) ⑶存在
⑶存在二十世紀.files/image203.gif) 。
。
20、⑴二十世紀.files/image205.gif)
⑵二十世紀.files/image207.gif) 或
或二十世紀.files/image209.gif)
⑶(二十世紀.files/image211.gif) ,
,二十世紀.files/image213.gif) )
)
附加題選修參考答案
1、⑴BB二十世紀.files/image215.gif) =
=二十世紀.files/image217.gif) , ⑵
, ⑵
二十世紀.files/image219.gif)
2、⑴二十世紀.files/image221.gif) ⑵
⑵ 二十世紀.files/image223.gif) ,
,二十世紀.files/image225.gif) ,
,二十世紀.files/image227.gif) ,EX=1
,EX=1
3、 二十世紀.files/image229.gif)
4、⑴ ⑵ MN=2
5、⑴特征值為2和3 ,對應的特征向量分別為二十世紀.files/image231.gif) 及
及二十世紀.files/image233.gif) ,
,
⑵ 二十世紀.files/image235.gif) ,橢圓在矩陣的作用下對應得新方程為
,橢圓在矩陣的作用下對應得新方程為二十世紀.files/image237.gif)
6、提示:二十世紀.files/image239.gif) ,然后用基本不等式或柯西不等式即可。
,然后用基本不等式或柯西不等式即可。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com