日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

如圖，在三棱柱中，側(cè)面，為棱上異于的一點，，已知，求：

（Ⅰ）異面直線與的距離；

（Ⅱ）二面角的平面角的正切值.

【解析】第一問中，利用建立空間直角坐標系

解：（I）以B為原點，、分別為Y,Z軸建立空間直角坐標系.由于，

在三棱柱中有

,

設

又側(cè)面，故. 因此是異面直線的公垂線，則，故異面直線的距離為1.

（II）由已知有故二面角的平面角的大小為向量與的夾角.

 

如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1.

（Ⅰ）證明PC⊥AD；

（Ⅱ）求二面角A-PC-D的正弦值；

（Ⅲ）設E為棱PA上的點，滿足異面直線BE與CD所成的角為30°，求AE的長.

 

【解析】解法一：如圖，以點A為原點建立空間直角坐標系，依題意得A(0,0,0)，D(2,0,0),C(0,1,0), 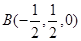,P（0,0,2）.

（1）證明：易得，于是,所以

(2) ,設平面PCD的法向量，

則,即.不防設，可得.可取平面PAC的法向量于是從而.

所以二面角A-PC-D的正弦值為.

（3）設點E的坐標為（0,0，h），其中，由此得.

由，故 

所以，，解得，即.

解法二：（1）證明：由，可得，又由,,故.又,所以.

(2)如圖，作于點H，連接DH.由,,可得.

因此,從而為二面角A-PC-D的平面角.在中，,由此得由（1）知,故在中，

因此所以二面角的正弦值為.

（3）如圖，因為，故過點B作CD的平行線必與線段AD相交，設交點為F，連接BE，EF. 故或其補角為異面直線BE與CD所成的角.由于BF∥CD，故.在中，故

在中，由,,

可得.由余弦定理，,

所以.

 

已知函數(shù)f(x)=e^x-ax，其中a＞0.

（1）若對一切x∈R，f(x) 1恒成立，求a的取值集合；

（2)在函數(shù)f(x)的圖像上去定點A（x₁, f(x₁)）,B(x₂, f(x₂))(x₁<x₂)，記直線AB的斜率為k，證明：存在x₀∈（x₁,x₂）,使恒成立.

【解析】解：令.

當時單調(diào)遞減；當時單調(diào)遞增，故當時，取最小值

于是對一切恒成立，當且僅當.　　　　　　　　①

令則

當時，單調(diào)遞增；當時，單調(diào)遞減.

故當時，取最大值.因此，當且僅當時，①式成立.

綜上所述，的取值集合為.

（Ⅱ）由題意知，令則

令，則.當時，單調(diào)遞減；當時，單調(diào)遞增.故當，即

從而，又

所以因為函數(shù)在區(qū)間上的圖像是連續(xù)不斷的一條曲線，所以存在使即成立.

【點評】本題考查利用導函數(shù)研究函數(shù)單調(diào)性、最值、不等式恒成立問題等，考查運算能力，考查分類討論思想、函數(shù)與方程思想等數(shù)學方法.第一問利用導函數(shù)法求出取最小值對一切x∈R，f(x) 1恒成立轉(zhuǎn)化為從而得出求a的取值集合；第二問在假設存在的情況下進行推理，然后把問題歸結(jié)為一個方程是否存在解的問題，通過構(gòu)造函數(shù)，研究這個函數(shù)的性質(zhì)進行分析判斷.

 

已知函數(shù)的圖象過坐標原點O,且在點處的切線的斜率是.

（Ⅰ）求實數(shù)的值； 

（Ⅱ）求在區(qū)間上的最大值；

（Ⅲ）對任意給定的正實數(shù)，曲線上是否存在兩點P、Q，使得是以O為直角頂點的直角三角形，且此三角形斜邊中點在軸上？說明理由.

【解析】第一問當時，，則。

依題意得：，即    解得

第二問當時，，令得，結(jié)合導數(shù)和函數(shù)之間的關(guān)系得到單調(diào)性的判定，得到極值和最值

第三問假設曲線上存在兩點P、Q滿足題設要求，則點P、Q只能在軸兩側(cè)。

不妨設，則，顯然

∵是以O為直角頂點的直角三角形，∴

即    （*）若方程（*）有解，存在滿足題設要求的兩點P、Q；

若方程（*）無解，不存在滿足題設要求的兩點P、Q.

（Ⅰ）當時，，則。

依題意得：，即    解得

（Ⅱ）由（Ⅰ）知，

①當時，，令得

當變化時，的變化情況如下表：

		0
	—	0	+	0	—
	單調(diào)遞減	極小值	單調(diào)遞增	極大值	單調(diào)遞減

又，，。∴在上的最大值為2.

②當時, .當時, ,最大值為0；

當時, 在上單調(diào)遞增。∴在最大值為。

綜上，當時，即時，在區(qū)間上的最大值為2；

當時，即時，在區(qū)間上的最大值為。

（Ⅲ）假設曲線上存在兩點P、Q滿足題設要求，則點P、Q只能在軸兩側(cè)。

不妨設，則，顯然

∵是以O為直角頂點的直角三角形，∴

即    （*）若方程（*）有解，存在滿足題設要求的兩點P、Q；

若方程（*）無解，不存在滿足題設要求的兩點P、Q.

若，則代入（*）式得：

即，而此方程無解，因此。此時，

代入（*）式得：    即   （**）

令 ，則

∴在上單調(diào)遞增，  ∵     ∴,∴的取值范圍是。

∴對于，方程（**）總有解，即方程（*）總有解。

因此，對任意給定的正實數(shù)，曲線上存在兩點P、Q，使得是以O為直角頂點的直角三角形，且此三角形斜邊中點在軸上