
題目列表(包括答案和解析)
在圓錐曲線的學習中,我們已經學習了它的標準方程,以橢圓![]() =1(a>b>0)為例說明此方程就是以F1(-c,0),F2(c,0)為焦點,長軸長為2a的橢圓的方程.怎樣利用曲線與方程的定義說明上述問題?
=1(a>b>0)為例說明此方程就是以F1(-c,0),F2(c,0)為焦點,長軸長為2a的橢圓的方程.怎樣利用曲線與方程的定義說明上述問題?
 (2013•浦東新區二模)(1)設橢圓C1:
(2013•浦東新區二模)(1)設橢圓C1:| x2 |
| a2 |
| y2 |
| b2 |
| 9y2 |
| 8 |
|
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| r1 |
| r2 |
| ||
| 3 |
| x2 |
| 25 |
| y2 |
| 16 |
| |AB| |
| |FM| |
| 10 |
| 3 |
| x2 |
| 25 |
| y2 |
| 16 |
| |AB| |
| |F1M| |
| 10 |
| 3 |
(1)設橢圓 :
: 與雙曲線
與雙曲線 :
: 有相同的焦點
有相同的焦點 ,
, 是橢圓
是橢圓 與雙曲線
與雙曲線 的公共點,且
的公共點,且 的周長為
的周長為 ,求橢圓
,求橢圓 的方程;
的方程;
我們把具有公共焦點、公共對稱軸的兩段圓錐曲線弧合成的封閉曲線稱為“盾圓”.
(2)如圖,已知“盾圓 ”的方程為
”的方程為 .設“盾圓
.設“盾圓 ”上的任意一點
”上的任意一點 到
到 的距離為
的距離為 ,
, 到直線
到直線 的距離為
的距離為 ,求證:
,求證: 為定值;
為定值;

(3)由拋物線弧 :
: (
(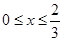 )與第(1)小題橢圓弧
)與第(1)小題橢圓弧 :
: (
( )所合成的封閉曲線為“盾圓
)所合成的封閉曲線為“盾圓 ”.設過點
”.設過點 的直線與“盾圓
的直線與“盾圓 ”交于
”交于 兩點,
兩點, ,
,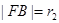 且
且 (
( ),試用
),試用 表示
表示 ;并求
;并求 的取值范圍.
的取值范圍.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com