日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

若·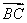+<0,則△ABC必定是(　　)

(A)銳角三角形 (B)鈍角三角形

(C)直角三角形 (D)等腰直角三角形

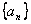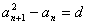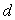 如果一個實數數列滿足條件：（為常數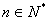，），則稱這一數列 “偽等差數列”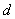， 稱為“偽公差”。給出下列關于某個偽等差數列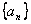的結論：

①對于任意的首項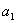，若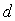<0,則這一數列必為有窮數列；

②當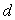>0, 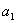>0時，這一數列必為單調遞增數列；

③這一數列可以是一個周期數列；

④若這一數列的首項為1，偽公差為3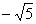，可以是這一數列中的一項；

⑤若這一數列的首項為0，第三項為-1，則這一數列的偽公差可以是。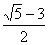

其中正確的結論是­­________________.

若二次函數f(x)=ax2+bx+c(a≠0)的圖象和直線y=x無交點,現有下列結論:①方程f(f(x))=x一定沒有實數根;

②若a>0,則不等式f(f(x))>x對一切實數x都成立;

③若a<0,則必存在實數x0,使f(f(x0))>x0;

④若a+b+c=0,則不等式f(f(x))<x對一切實數都成立;

⑤函數g(x)=ax2-bx+c的圖象與直線y=-x也一定沒有交點.

其中正確的結論是　　　　(寫出所有正確結論的編號). 

若<<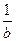0, 則（1）a+ b < a b,  (2)|a|>|b|,  (3)a<b,  (4)中正確的有___________.

16．(2)解（1）當a=1,b=-2時，g(x)=f(x)-2,把f(x)圖象向下平移兩個單位就可得到g(x)圖象，

這時函數g(x)只有兩個零點，所以（1）不對

（2）若a=-1,-2<b<0,則把函數f(x)作關于x軸對稱圖象，然后向下平移不超過2個單位就可得到g(x)圖象，這時g(x)有超過2的零點

（3）當a<0時， y=af(x)根據定義可斷定是奇函數，如果b≠0，把奇函數y=af(x)圖象再向上（或向下）平移后才是y=g(x)=af(x)+b的圖象，那么肯定不會再關于原點對稱了，肯定不是奇函數；當b=0時才是奇函數，所以(3)不對。所以正確的只有(2)

一盒中放有大小相同的紅色、綠色、黃色三種小球，已知紅球個數是綠球個數的兩倍，黃球個數是綠球個數的一半，現在從該盒中隨機取出一球，若取出紅球得1分，取出黃球得0分，取出綠球得-1分，試寫出從該盒中取出一球所得分數Y的分布列.