
題目列表(包括答案和解析)
(本小題滿分14分)
已知函數![]() 對于任意
對于任意![]() (
(![]() ),都有式子
),都有式子![]() 成立(其中
成立(其中![]() 為常數).
為常數).
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)利用函數![]() 構造一個數列,方法如下:
構造一個數列,方法如下:
對于給定的定義域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述構造過程中,如果![]() (
(![]() =1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果
=1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果![]() 不在定義域中,那么構造數列的過程就停止.
不在定義域中,那么構造數列的過程就停止.
(ⅰ)如果可以用上述方法構造出一個常數列,求![]() 的取值范圍;
的取值范圍;
(ⅱ)是否存在一個實數![]() ,使得取定義域中的任一值作為
,使得取定義域中的任一值作為![]() ,都可用上述方法構造出一個無窮數列
,都可用上述方法構造出一個無窮數列![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(ⅲ)當![]() 時,若
時,若![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
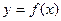 對于任意
對于任意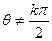 (
(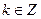 ),都有式子
),都有式子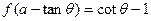 成立(其中
成立(其中 為常數).
為常數).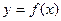 的解析式;
的解析式; 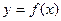 構造一個數列,方法如下:
構造一個數列,方法如下: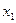 ,令
,令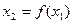 ,
,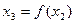 ,…,
,…,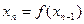 ,…
,… 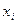 (
(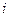 =1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果
=1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果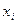 不在定義域中,那么構造數列的過程就停止.
不在定義域中,那么構造數列的過程就停止. 的取值范圍;
的取值范圍; ,使得取定義域中的任一值作為
,使得取定義域中的任一值作為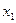 ,都可用上述方法構造出一個無窮數列
,都可用上述方法構造出一個無窮數列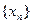 ?若存在,求出
?若存在,求出 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;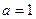 時,若
時,若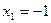 ,求數列
,求數列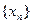 的通項公式.
的通項公式.已知函數y=f(x)對于任意![]() (k∈Z),都有式子f(a-tanθ)=cotθ-1成立(其中a為常數).
(k∈Z),都有式子f(a-tanθ)=cotθ-1成立(其中a為常數).
(Ⅰ)求函數y=f(x)的解析式;
(Ⅱ)利用函數y=f(x)構造一個數列,方法如下:
對于給定的定義域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…在上述構造過程中,如果xi(i=1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果xi不在定義域中,那么構造數列的過程就停止.
(ⅰ)如果可以用上述方法構造出一個常數列,求a的取值范圍;
(ⅱ)是否存在一個實數a,使得取定義域中的任一值作為x1,都可用上述方法構造出一個無窮數列{xn}?若存在,求出a的值;若不存在,請說明理由;
(ⅲ)當a=1時,若x1=-1,求數列{xn}的通項公式.
| kπ | 2 |
已知函數 的最小值為0,其中
的最小值為0,其中
(Ⅰ)求 的值;
的值;
(Ⅱ)若對任意的 有
有 ≤
≤ 成立,求實數
成立,求實數 的最小值;
的最小值;
(Ⅲ)證明 (
( ).
).
【解析】(1)解:
 的定義域為
的定義域為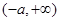

由 ,得
,得
當x變化時, ,
, 的變化情況如下表:
的變化情況如下表:
|
x |
|
|
|
|
|
- |
0 |
+ |
|
|
|
極小值 |
|
因此, 在
在 處取得最小值,故由題意
處取得最小值,故由題意 ,所以
,所以
(2)解:當 時,取
時,取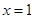 ,有
,有 ,故
,故 時不合題意.當
時不合題意.當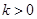 時,令
時,令 ,即
,即

令 ,得
,得
①當 時,
時, ,
, 在
在 上恒成立。因此
上恒成立。因此 在
在 上單調遞減.從而對于任意的
上單調遞減.從而對于任意的 ,總有
,總有 ,即
,即 在
在 上恒成立,故
上恒成立,故 符合題意.
符合題意.
②當 時,
時, ,對于
,對于 ,
, ,故
,故 在
在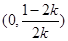 上單調遞增.因此當取
上單調遞增.因此當取 時,
時, ,即
,即 不成立.
不成立.
故 不合題意.
不合題意.
綜上,k的最小值為 .
.
(3)證明:當n=1時,不等式左邊= =右邊,所以不等式成立.
=右邊,所以不等式成立.
當 時,
時,


在(2)中取 ,得
,得
 ,
,
從而

所以有





綜上,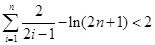 ,
,
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com