
題目列表(包括答案和解析)

對于上面給出的四個圖象,以下說法正確的是
A.①反映了建議(2),③反映了建議(1) B.①反映了建議(1),③反映了建議(2)
C.②反映了建議(1),③反映了建議(2) D.④反映了建議(1),④反映了建議(1)
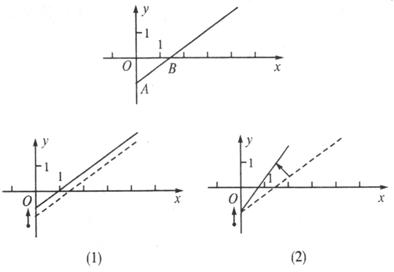
請你根據圖象用簡練的語言敘述:
建議(1)是_____________________________________________;
建議(2)是_____________________________________________.
下列可以看成算法的是( )
A.學習數學時,課前預習,課上認真聽講并記好筆記,課下先復習再做作業,之后做適當的練習題
B.今天餐廳的飯真好吃
C.這道數學題難做
D.方程2x2-x+1=0無實數根
|
| 2 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com