日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

在△ABC中，a、b、c分別是角A、B、C的對邊,cosB＝.

⑴ 若cosA＝－,求cosC的值；  ⑵ 若AC＝,BC＝5，求△ABC的面積.

【解析】第一問中sinB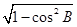＝＝, sinA＝＝

cosC＝cos(180°－A－B)＝－cos(A＋B)                ＝sinA.sinB－cosA·cosB

＝×－(－)×＝

第二問中，由＝＋－2AB×BC×cosB得 10＝＋25－8AB

解得AB＝5或AB＝3綜合得△ABC的面積為或

解：⑴ sinB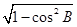＝＝, sinA＝＝,………………2分

∴cosC＝cos(180°－A－B)＝－cos(A＋B)                  ……………………3分

＝sinA.sinB－cosA·cosB                            ……………………4分

＝×－(－)×＝                   ……………………6分

⑵ 由＝＋－2AB×BC×cosB得 10＝＋25－8AB   ………………7分

解得AB＝5或AB＝3，                               ……………………9分

若AB＝5，則S_△ABC＝AB×BC×sinB＝×5×5×＝    ………………10分

若AB＝3，則S_△ABC＝AB×BC×sinB＝×5×3×＝……………………11分

綜合得△ABC的面積為或

(1)兩個長度相等的向量一定相等；

[　　]

(2)相等的向量起點必相同；

[　　]

(3)平行向量就是共線向量；

[　　]

(4)若向量a的模小于b的模，則a＜b；

[　　]

(5)質量、動量、功、加速度都是向量；

[　　]

(6)與共線，則A，B，C，D四點必在一條直線上；

[　　]

(7)向量a與b平行，則a與b的方向相同或相反；

[　　]

(8)在△ABC中，；

[　　]

(9)若向量a與b有共同的起點，則以b的終點為起點，以a的終點為終點的向量等于b－a；

[　　]

(10)若且b≠0，當a＝時，則一定有a，b共線；

[　　]

(11)若a·b＝0，則或；

[　　]

(12)若a·b＝a·c，且a≠0，則b＝c；

[　　]

(13)向量a在b方向上的射影是一個模等于(是a與b的夾角)，方向與b相同或相反的向量；

[　　]

(14)．

[　　]