日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（本小題滿分12分）

第16屆亞運會將于今年11月在我市舉行，射擊隊運動員們正在積極備戰. 若某運動員每次射擊成績為10環的概率為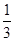. 求該運動員在5次射擊中，

（1）恰有3次射擊成績為10環的概率；

（2）至少有3次射擊成績為10環的概率；

（3）射擊成績為10環的均值（數學期望）.

（結果用分數表示）

（本小題滿分12分）某射擊運動員在一次射擊中，命中10環、9環、8環、7環的概率分別為0.2、0.35、0.2、0.15。求此運動員

（1）在一次射擊中，命中10環或9環的概率。

（2）在一次射擊中，命中環數小于8環的概率。

（3）在兩次射擊中，至少有一次擊中10環的概率。

（本小題滿分12分）甲、乙兩運動員進行射擊訓練，已知他們擊中的環數都穩定在7，8，9，10環，且每次射擊成績互不影響．射擊環數的頻率分布條形圖如下：

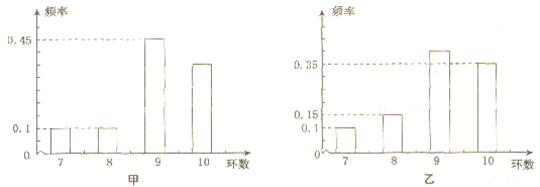
若將頻率視為概率，回答下列問題．(Ⅰ)求甲運動員在3次射擊中至少有1次擊中9環以上(含9環)的概率； (Ⅱ)若甲、乙兩運動員各自射擊1次，ξ表示這2次射擊中擊中9環以上(含9環)的次數，求ξ的分布列及Eξ．

（08年衡陽八中理） (12分） 甲、乙兩名射擊運動員，甲射擊一次命中10環的概率為，乙射擊一次命中10環的概率為s，若他們各自獨立地射擊兩次，設乙命中10環的次數為ξ，且ξ的數學期望Eξ=，表示甲與乙命中10環的次數的差的絕對值.

    (1)求s的值及的分布列，

    (2)求的數學期望.

(本小題滿分12分)

甲、乙兩名射擊運動員，甲射擊一次命中10環的概率為，乙射擊一次命中10環的概率為s，若他們各自獨立地射擊兩次，設乙命中10環的次數為ξ，且ξ的數學期望Eξ=，表示甲與乙命中10環的次數的差的絕對值.

    (1)求s的值及的分布列，   (2)求的數學期望.