日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

已知直三棱柱中, , ， 是和的交點, 若.

（1）求的長；  （2）求點到平面的距離；

（3）求二面角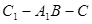的平面角的正弦值的大小.

【解析】本試題主要考查了距離和角的求解運用。第一問中，利用ACCA為正方形, AC=3

第二問中，利用面BBCC內作CDBC, 則CD就是點C平面ABC的距離CD=，第三問中，利用三垂線定理作二面角的平面角，然后利用直角三角形求解得到其正弦值為

解法一: (1)連AC交AC于E, 易證ACCA為正方形, AC=3 ……………  5分

(2)在面BBCC內作CDBC, 則CD就是點C平面ABC的距離CD= … 8分

(3) 易得AC面ACB, 過E作EHAB于H, 連HC, 則HCAB

CHE為二面角C－AB－C的平面角. ………  9分

sinCHE=二面角C－AB－C的平面角的正弦大小為 ……… 12分

解法二: (1)分別以直線CB、CC、CA為x、y為軸建立空間直角坐標系, 設|CA|=h, 則C(0, 0, 0), B(4, 0, 0), B(4, －3, 0), C(0, －3, 0), A(0, 0, h), A(0, －3, h), G(2, －, －) ………………………  3分

=(2, －, －), =(0, －3, －h)  ……… 4分

·=0,  h=3

(2)設平面ABC得法向量=(a, b, c),則可求得=(3, 4, 0) (令a=3)

點A到平面ABC的距離為H=||=……… 8分

(3) 設平面ABC的法向量為=(x, y, z),則可求得=(0, 1, 1) (令z=1)

二面角C－AB－C的大小滿足cos== ………  11分

二面角C－AB－C的平面角的正弦大小為

（本小題滿分12分）

為了測量兩山頂M，N間的距離，飛機沿水平方向在A，B兩點進行測量，A，B，M，N在同一個鉛垂平面內（如示意圖），飛機能夠測量的數據有俯角和A，B間的距離，請設計一個方案，包括：①指出需要測量的數據（用字母表示，并在圖中標出）；②用文字和公式寫出計算M，N間的距離的步驟。

（本題滿分12分）已知對任意的平面向量，把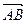繞其起點沿逆時針方向旋轉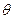角，得到向量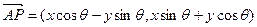，叫做把點B繞點A逆時針方向旋轉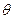角得到點P
①已知平面內的點A（1，2），B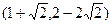，把點B繞點A沿逆時針方向旋轉后得到點P，求點P的坐標
②設平面內曲線C上的每一點繞逆時針方向旋轉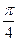后得到的點的軌跡是曲線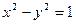，求原來曲線C的方程.

（（本小題滿分12分）設x，y∈R，，為直角坐標平面內x，y軸正方向上單位向量，若

向量，，且．

（1）求點M（x，y）的軌跡C的方程；

（2）若直線L與曲線C交于A、B兩點，若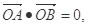求證直線L與某個定圓E相切，并求出定圓E的方程。