
題目列表(包括答案和解析)
 分享到
分享到百度分享
一個有一定厚度的圓盤,可以繞通過中心垂直于盤面的水平軸轉動,用下面的方法測量它勻速轉動時的角速度。
實驗器材:電磁打點計時器、米尺、紙帶、復寫紙片。
實驗步驟:
(1)如圖1所示,將電磁打點計時器固定在桌面上,將紙帶的一端穿過打點計時器的限位孔后,固定在待測圓盤的側面上,使得圓盤轉動時,紙帶可以卷在圓盤側面上。
(2)啟動控制裝置使圓盤轉動,同時接通電源,打點計時器開始打點。
(3)經過一段時間,停止轉動和打點,取下紙帶,進行測量。
① 由已知量和測得量表示的角速度的表達式為ω= 。式中各量的意義是:
.
② 某次實驗測得圓盤半徑r=5.50×10-2m,得到紙帶的一段如圖2所示,求得角速度為 。
(1) (2)6.8/s。 |
第Ⅰ卷(選擇題 共31分)
一、單項選擇題.本題共5小題,每小題3分,共計15分.每小題只有一個選項符合題意.
1. 關于科學家和他們的貢獻,下列說法中正確的是[來源:Www..com]
A.安培首先發現了電流的磁效應
B.伽利略認為自由落體運動是速度隨位移均勻變化的運動
C.牛頓發現了萬有引力定律,并計算出太陽與地球間引力的大小
D.法拉第提出了電場的觀點,說明處于電場中電荷所受到的力是電場給予的
2.如圖為一種主動式光控報警器原理圖,圖中R1和R2為光敏電阻,R3和R4為定值電阻.當射向光敏電阻R1和R2的任何一束光線被遮擋時,都會引起警鈴發聲,則圖中虛線框內的電路是
A.與門 B.或門 C.或非門 D.與非門
 | |||
 | |||
3.如圖所示的交流電路中,理想變壓器原線圈輸入電壓為U1,輸入功率為P1,輸出功率為P2,各交流電表均為理想電表.當滑動變阻器R的滑動頭向下移動時
A.燈L變亮 B.各個電表讀數均變大
C.因為U1不變,所以P1不變 D.P1變大,且始終有P1= P2
 4.豎直平面內光滑圓軌道外側,一小球以某一水平速度v0從A點出發沿圓軌道運動,至B點時脫離軌道,最終落在水平面上的C點,不計空氣阻力.下列說法中不正確的是
4.豎直平面內光滑圓軌道外側,一小球以某一水平速度v0從A點出發沿圓軌道運動,至B點時脫離軌道,最終落在水平面上的C點,不計空氣阻力.下列說法中不正確的是
A.在B點時,小球對圓軌道的壓力為零
B.B到C過程,小球做勻變速運動
C.在A點時,小球對圓軌道壓力大于其重力
D.A到B過程,小球水平方向的加速度先增加后減小
 5.如圖所示,水平面上放置質量為M的三角形斜劈,斜劈頂端安裝光滑的定滑輪,細繩跨過定滑輪分別連接質量為m1和m2的物塊.m1在斜面上運動,三角形斜劈保持靜止狀態.下列說法中正確的是
5.如圖所示,水平面上放置質量為M的三角形斜劈,斜劈頂端安裝光滑的定滑輪,細繩跨過定滑輪分別連接質量為m1和m2的物塊.m1在斜面上運動,三角形斜劈保持靜止狀態.下列說法中正確的是
A.若m2向下運動,則斜劈受到水平面向左摩擦力
B.若m1沿斜面向下加速運動,則斜劈受到水平面向右的摩擦力
C.若m1沿斜面向下運動,則斜劈受到水平面的支持力大于(m1+ m2+M)g
D.若m2向上運動,則輕繩的拉力一定大于m2g
二、多項選擇題.本題共4小題,每小題4分,共計16分.每小題有多個選項符合題意.全部選對的得4分,選對但不全的得2分,錯選或不答的得0分.
6.木星是太陽系中最大的行星,它有眾多衛星.觀察測出:木星繞太陽作圓周運動的半徑為r1、 周期為T1;木星的某一衛星繞木星作圓周運動的半徑為r2、 周期為T2.已知萬有引力常量為G,則根據題中給定條件
A.能求出木星的質量
B.能求出木星與衛星間的萬有引力
C.能求出太陽與木星間的萬有引力
D.可以斷定![]()
 7.如圖所示,xOy坐標平面在豎直面內,x軸沿水平方向,y軸正方向豎直向上,在圖示空間內有垂直于xOy平面的水平勻強磁場.一帶電小球從O點由靜止釋放,運動軌跡如圖中曲線.關于帶電小球的運動,下列說法中正確的是
7.如圖所示,xOy坐標平面在豎直面內,x軸沿水平方向,y軸正方向豎直向上,在圖示空間內有垂直于xOy平面的水平勻強磁場.一帶電小球從O點由靜止釋放,運動軌跡如圖中曲線.關于帶電小球的運動,下列說法中正確的是
A.OAB軌跡為半圓
B.小球運動至最低點A時速度最大,且沿水平方向
C.小球在整個運動過程中機械能守恒
D.小球在A點時受到的洛倫茲力與重力大小相等
 8.如圖所示,質量為M、長為L的木板置于光滑的水平面上,一質量為m的滑塊放置在木板左端,滑塊與木板間滑動摩擦力大小為f,用水平的恒定拉力F作用于滑塊.當滑塊運動到木板右端時,木板在地面上移動的距離為s,滑塊速度為v1,木板速度為v2,下列結論中正確的是
8.如圖所示,質量為M、長為L的木板置于光滑的水平面上,一質量為m的滑塊放置在木板左端,滑塊與木板間滑動摩擦力大小為f,用水平的恒定拉力F作用于滑塊.當滑塊運動到木板右端時,木板在地面上移動的距離為s,滑塊速度為v1,木板速度為v2,下列結論中正確的是
A.上述過程中,F做功大小為![]()
B.其他條件不變的情況下,F越大,滑塊到達右端所用時間越長
C.其他條件不變的情況下,M越大,s越小
D.其他條件不變的情況下,f越大,滑塊與木板間產生的熱量越多
9.如圖所示,兩個固定的相同細環相距一定的距離,同軸放置,O1、O2分別為兩環的圓心,兩環分別帶有均勻分布的等量異種電荷.一帶正電的粒子從很遠處沿軸線飛來并穿過兩環.則在帶電粒子運動過程中
A.在O1點粒子加速度方向向左
B.從O1到O2過程粒子電勢能一直增加
C.軸線上O1點右側存在一點,粒子在該點動能最小
D.軸線上O1點右側、O2點左側都存在場強為零的點,它們關于O1、O2連線中點對稱
 |
第Ⅱ卷(非選擇題 共89分)
三、簡答題:本題分必做題(第lO、11題)和選做題(第12題)兩部分,共計42分.請將解答填寫在答題卡相應的位置.
必做題
10.測定木塊與長木板之間的動摩擦因數時,采用如圖所示的裝置,圖中長木板水平固定.
 (1)實驗過程中,電火花計時器應接在 ▲ (選填“直流”或“交流”)電源上.調整定滑輪高度,使 ▲ .
(1)實驗過程中,電火花計時器應接在 ▲ (選填“直流”或“交流”)電源上.調整定滑輪高度,使 ▲ .
(2)已知重力加速度為g,測得木塊的質量為M,砝碼盤和砝碼的總質量為m,木塊的加速度為a,則木塊與長木板間動摩擦因數μ= ▲ .
(3)如圖為木塊在水平木板上帶動紙帶運動打出的一條紙帶的一部分,0、1、2、3、4、5、6為計數點,相鄰兩計數點間還有4個打點未畫出.從紙帶上測出x1=3.20cm,x2=4.52cm,x5=8.42cm,x6=9.70cm.則木塊加速度大小a= ▲ m/s2(保留兩位有效數字).
 |
11.為了測量某電池的電動勢 E(約為3V)和內阻 r,可供選擇的器材如下:
A.電流表G1(2mA 100Ω) B.電流表G2(1mA 內阻未知)
C.電阻箱R1(0~999.9Ω) D.電阻箱R2(0~9999Ω)
E.滑動變阻器R3(0~10Ω 1A) F.滑動變阻器R4(0~1000Ω 10mA)
G.定值電阻R0(800Ω 0.1A) H.待測電池
I.導線、電鍵若干
 (1)采用如圖甲所示的電路,測定電流表G2的內阻,得到電流表G1的示數I1、電流表G2的示數I2如下表所示:
(1)采用如圖甲所示的電路,測定電流表G2的內阻,得到電流表G1的示數I1、電流表G2的示數I2如下表所示:
| I1(mA) | 0.40 | 0.81 | 1.20 | 1.59 | 2.00 |
| I2(mA) | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
 |
根據測量數據,請在圖乙坐標中描點作出I1—I2圖線.由圖得到電流表G2的內阻等于
▲ Ω.
(2)在現有器材的條件下,測量該電池電動勢和內阻,采用如圖丙所示的電路,圖中滑動變阻器①應該選用給定的器材中 ▲ ,電阻箱②選 ▲ (均填寫器材代號).
(3)根據圖丙所示電路,請在丁圖中用筆畫線代替導線,完成實物電路的連接.
 | |||
 | |||
12.選做題(請從A、B和C三小題中選定兩小題作答,并在答題卡上把所選題目對應字母后的方框涂滿涂黑.如都作答,則按A、B兩小題評分.)
A.(選修模塊3-3)(12分)
(1)下列說法中正確的是 ▲
A.液體表面層分子間距離大于液體內部分子間距離,液體表面存在張力
B.擴散運動就是布朗運動
C.蔗糖受潮后會粘在一起,沒有確定的幾何形狀,它是非晶體
D.對任何一類與熱現象有關的宏觀自然過程進行方向的說明,都可以作為熱力學第二定律的表述
(2)將1ml的純油酸加到500ml的酒精中,待均勻溶解后,用滴管取1ml油酸酒精溶液,讓其自然滴出,共200滴.現在讓其中一滴落到盛水的淺盤內,待油膜充分展開后,測得油膜的面積為200cm2,則估算油酸分子的大小是 ▲ m(保留一位有效數字).
 (3)如圖所示,一直立的汽缸用一質量為m的活塞封閉一定量的理想氣體,活塞橫截面積為S,汽缸內壁光滑且缸壁是導熱的,開始活塞被固定,打開固定螺栓K,活塞下落,經過足夠長時間后,活塞停在B點,已知AB=h,大氣壓強為p0,重力加速度為g.
(3)如圖所示,一直立的汽缸用一質量為m的活塞封閉一定量的理想氣體,活塞橫截面積為S,汽缸內壁光滑且缸壁是導熱的,開始活塞被固定,打開固定螺栓K,活塞下落,經過足夠長時間后,活塞停在B點,已知AB=h,大氣壓強為p0,重力加速度為g.
①求活塞停在B點時缸內封閉氣體的壓強;
②設周圍環境溫度保持不變,求整個過程中通過缸壁傳遞的熱量Q(一定量理想氣體的內能僅由溫度決定).
B.(選修模塊3-4)(12分)
(1)下列說法中正確的是 ▲
A.照相機、攝影機鏡頭表面涂有增透膜,利用了光的干涉原理
B.光照射遮擋物形成的影輪廓模糊,是光的衍射現象
 C.太陽光是偏振光
C.太陽光是偏振光
D.為了有效地發射電磁波,應該采用長波發射
(2)甲、乙兩人站在地面上時身高都是L0, 甲、乙分別乘坐速度為0.6c和0.8c(c為光速)的飛船同向運動,如圖所示.此時乙觀察到甲的身高L ▲ L0;若甲向乙揮手,動作時間為t0,乙觀察到甲動作時間為t1,則t1 ▲ t0(均選填“>”、“ =” 或“<”).
(3)x=0的質點在t=0時刻開始振動,產生的波沿x軸正方向傳播,t1=0.14s時刻波的圖象如圖所示,質點A剛好開始振動.
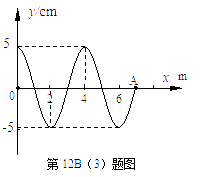 ①求波在介質中的傳播速度;
①求波在介質中的傳播速度;
②求x=4m的質點在0.14s內運動的路程.
C.(選修模塊3-5)(12分)
(1)下列說法中正確的是 ▲
A.康普頓效應進一步證實了光的波動特性
B.為了解釋黑體輻射規律,普朗克提出電磁輻射的能量是量子化的
C.經典物理學不能解釋原子的穩定性和原子光譜的分立特征
D.天然放射性元素衰變的快慢與化學、物理狀態有關
(2)![]() 是不穩定的,能自發的發生衰變.
是不穩定的,能自發的發生衰變.
①完成![]() 衰變反應方程
衰變反應方程 ![]() ▲ .
▲ .
②![]() 衰變為
衰變為![]() ,經過 ▲ 次α衰變, ▲ 次β衰變.
,經過 ▲ 次α衰變, ▲ 次β衰變.
(3)1919年,盧瑟福用α粒子轟擊氮核發現質子.科學研究表明其核反應過程是:α粒子轟擊靜止的氮核后形成了不穩定的復核,復核發生衰變放出質子,變成氧核.設α粒子質量為m1,初速度為v0,氮核質量為m2,質子質量為m0, 氧核的質量為m3,不考慮相對論效應.
①α粒子轟擊氮核形成不穩定復核的瞬間,復核的速度為多大?
②求此過程中釋放的核能.
四、計算題:本題共3小題,共計47分.解答時請寫出必要的文字說明、方程式和重要的演算步驟,只寫出最后答案的不能得分,有數值計算的題,答案中必須明確寫出數值和單位.
13.如圖所示,一質量為m的氫氣球用細繩拴在地面上,地面上空風速水平且恒為v0,球靜止時繩與水平方向夾角為α.某時刻繩突然斷裂,氫氣球飛走.已知氫氣球在空氣中運動時所受到的阻力f正比于其相對空氣的速度v,可以表示為f=kv(k為已知的常數).則
(1)氫氣球受到的浮力為多大?
(2)繩斷裂瞬間,氫氣球加速度為多大?
(3)一段時間后氫氣球在空中做勻速直線運動,其水平方向上的速度與風速v0相等,求此時氣球速度大小(設空氣密度不發生變化,重力加速度為g).
 |
14.如圖所示,光滑絕緣水平面上放置一均勻導體制成的正方形線框abcd,線框質量為m,電阻為R,邊長為L.有一方向豎直向下的有界磁場,磁場的磁感應強度為B,磁場區寬度大于L,左邊界與ab邊平行.線框在水平向右的拉力作用下垂直于邊界線穿過磁場區.
(1)若線框以速度v勻速穿過磁場區,求線框在離開磁場時ab兩點間的電勢差;
(2)若線框從靜止開始以恒定的加速度a運動,經過t1時間ab邊開始進入磁場,求cd邊將要進入磁場時刻回路的電功率;
(3)若線框以初速度v0進入磁場,且拉力的功率恒為P0.經過時間T,cd邊進入磁場,此過程中回路產生的電熱為Q.后來ab邊剛穿出磁場時,線框速度也為v0,求線框穿過磁場所用的時間t.

15.如圖所示,有界勻強磁場的磁感應強度為B,方向垂直紙面向里,MN為其左邊界,磁場中放置一半徑為R的圓柱形金屬圓筒,圓心O到MN的距離OO1=2R,圓筒軸線與磁場平行.圓筒用導線通過一個電阻r0接地,最初金屬圓筒不帶電.現有范圍足夠大的平行電子束以速度v0從很遠處沿垂直于左邊界MN向右射入磁場區,已知電子質量為m,電量為e.
(1)若電子初速度滿足![]() ,則在最初圓筒上沒有帶電時,能夠打到圓筒上的電子對應MN邊界上O1兩側的范圍是多大?
,則在最初圓筒上沒有帶電時,能夠打到圓筒上的電子對應MN邊界上O1兩側的范圍是多大?
(2)當圓筒上電量達到相對穩定時,測量得到通過電阻r0的電流恒為I,忽略運動電子間的相互作用,求此時金屬圓筒的電勢φ和電子到達圓筒時速度v(取無窮遠處或大地電勢為零).
(3)在(2)的情況下,求金屬圓筒的發熱功率.
 |
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com